题目内容
设数列{an}、{bn}满足a1=4,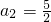 ,
,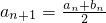 ,
, .
.
(Ⅰ) 证明:anbn=4
(Ⅱ) 证明:an>2,0<bn<2(n∈N*);
(Ⅲ)设 ,求数列{cn}的通项公式.
,求数列{cn}的通项公式.
(Ⅰ)证明:∵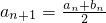 ,
,
∴两式相乘得anbn=an+1bn+1,
∴{anbn}为常数列,
∴anbn=a1b1=4;…(4分)
(Ⅱ) 证明:由(Ⅰ)知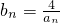 ,
,
∴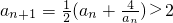 (若an=2,则an+1=2,从而可得{an}为常数列与a1=4矛盾),
(若an=2,则an+1=2,从而可得{an}为常数列与a1=4矛盾),
∴an>2,∴0<bn<2;…(8分)
(Ⅲ)解:∵ ,
,
∴
又因为c1=1,∴{cn}为等比数列,
∴ …(15分)
…(15分)
分析:(Ⅰ)将已知条件,两式相乘,可得{anbn}为常数列,从而可得结论;
(Ⅱ) 由(Ⅰ)知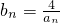 ,则
,则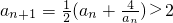 ,利用基本不等式可得结论;
,利用基本不等式可得结论;
(Ⅲ)利用 ,代入计算,可得{cn}为等比数列,从而可得数列{cn}的通项公式.
,代入计算,可得{cn}为等比数列,从而可得数列{cn}的通项公式.
点评:本题考查数列递推式,考查等比数列的判定,考查基本不等式的运用,属于中档题.
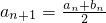 ,
,
∴两式相乘得anbn=an+1bn+1,
∴{anbn}为常数列,
∴anbn=a1b1=4;…(4分)
(Ⅱ) 证明:由(Ⅰ)知
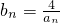 ,
,∴
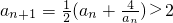 (若an=2,则an+1=2,从而可得{an}为常数列与a1=4矛盾),
(若an=2,则an+1=2,从而可得{an}为常数列与a1=4矛盾),∴an>2,∴0<bn<2;…(8分)
(Ⅲ)解:∵
 ,
,∴

又因为c1=1,∴{cn}为等比数列,
∴
 …(15分)
…(15分)分析:(Ⅰ)将已知条件,两式相乘,可得{anbn}为常数列,从而可得结论;
(Ⅱ) 由(Ⅰ)知
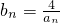 ,则
,则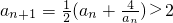 ,利用基本不等式可得结论;
,利用基本不等式可得结论;(Ⅲ)利用
 ,代入计算,可得{cn}为等比数列,从而可得数列{cn}的通项公式.
,代入计算,可得{cn}为等比数列,从而可得数列{cn}的通项公式.点评:本题考查数列递推式,考查等比数列的判定,考查基本不等式的运用,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目