题目内容
已知函数f(x)是以2为周期的偶函数,且当x∈(0,1)时,f(x)=2x-1,则f(log212)的值为( )A.

B.

C.2
D.11
【答案】分析:由于log212=2+log23,f(x)是以2为周期的偶函数⇒f(log212)=f(log23)=f(-log23)=f(2-log23),2-log23∈(0,1),从而可求得f(log212)的值.
解答:解:∵f(x)是以2为周期的偶函数,log212=2+log23,
∴f(log212)=f(log23)=f(-log23)=f(2-log23),
又2-log23∈(0,1),
∴f(2-log23)=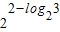 -1=
-1= -1=
-1= .
.
故需啊A.
点评:本题考查函数的周期性与奇偶性,难点在于利用函数的周期性与奇偶性将f(log212)转化为f(2-log23),属于中档题.
解答:解:∵f(x)是以2为周期的偶函数,log212=2+log23,
∴f(log212)=f(log23)=f(-log23)=f(2-log23),
又2-log23∈(0,1),
∴f(2-log23)=
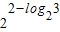 -1=
-1= -1=
-1= .
.故需啊A.
点评:本题考查函数的周期性与奇偶性,难点在于利用函数的周期性与奇偶性将f(log212)转化为f(2-log23),属于中档题.

练习册系列答案
相关题目
已知函数f(x)是以2为周期的偶函数,且当x∈(0,1)时,f(x)=2x-1,则f(log210)的值( )
A、
| ||
B、
| ||
C、-
| ||
D、-
|
 时,
时, ,则
,则 =
.
=
.