题目内容
已知实数a，b满足-1≤a≤1，-1≤b≤1，则函数f（x）=
x3-ax2+bx+5的两个极值点都在（0，1）内的概率为
．
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 12 |
分析：由题设知x2-2ax+b=0的两个根都在（0，1）内，作出区域-1≤a≤1，-1≤b≤1的面积和a2＞b在条件0＜a＜1，0＜b＜1下的面积，由此能求出结果．
解答：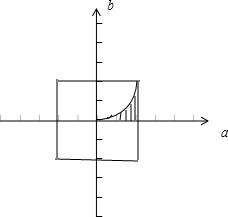
解：：∵函数f（x）=
x3-ax2+bx+5，
∴f′（x）=x2-2ax+b，
∵函数f（x）=
x3-ax2+bx+5的两个极值点都在（0，1）内，
x2-2ax+b=0的两个根都在（0，1）内，
∴两根之和2a∈（0，2），两根之积b∈（0，1），
∴
，
∵实数a，b满足-1≤a≤1，-1≤b≤1，
∴如图所示，区域-1≤a≤1，-1≤b≤1的面积（图中正方形所示）为4，
a2＞b在条件0＜a＜1，0＜b＜1下的面积（图中阴影所示）为：∫01x2dx=
x3|01=
．
∴
=
．
故答案为：
．
解：：∵函数f（x）=| 1 |
| 3 |
∴f′（x）=x2-2ax+b，
∵函数f（x）=
| 1 |
| 3 |
x2-2ax+b=0的两个根都在（0，1）内，
∴两根之和2a∈（0，2），两根之积b∈（0，1），
∴
|
∵实数a，b满足-1≤a≤1，-1≤b≤1，
∴如图所示，区域-1≤a≤1，-1≤b≤1的面积（图中正方形所示）为4，
a2＞b在条件0＜a＜1，0＜b＜1下的面积（图中阴影所示）为：∫01x2dx=
| 1 |
| 3 |
| 1 |
| 3 |
∴
| ||
| 4 |
| 1 |
| 12 |
故答案为：
| 1 |
| 12 |
点评：几何概型的概率估算公式中的“几何度量”，可以为线段长度、含面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据公式求解．
练习册系列答案
相关题目
已知实数a、b满足条件：ab＜0，且1是a2与b2的等比中项，又是
，
的等差中项，则
的值是（ ）
| 1 |
| a |
| 1 |
| b |
| a+b |
| a2+b2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|