题目内容
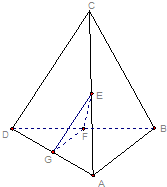四面体ABCD中，E、F分别是AC、BD的中点，若CD=2AB=2，EF⊥平面ABD，求EF与CD所成的角．
解：取AD的中点G，连接EG、FG，EG∥CD
∵CD=2AB=2，
易知EG=1，FG=
．
又∵EF⊥平面ABD，AB?平面ABD，
∴EF⊥AB
又∵GF∥AB知EF⊥FG．
在Rt△EFG中，
sin∠GEF=
=
∴∠GEF=30°，
即异面直线EF与CD所成的角为30°．
分析：取AD的中点G，连接EG、FG，将CD平移到EG，则∠GEF为异面EF与CD所成的角，再在Rt△EFG中，求出此角即可．
点评：本小题主要考查异面直线所成的角，考查空间想象能力、运算能力和推理论证能力，属于基础题．
∵CD=2AB=2，
易知EG=1，FG=
．又∵EF⊥平面ABD，AB?平面ABD，
∴EF⊥AB
又∵GF∥AB知EF⊥FG．
在Rt△EFG中，
sin∠GEF=
=∴∠GEF=30°，
即异面直线EF与CD所成的角为30°．
分析：取AD的中点G，连接EG、FG，将CD平移到EG，则∠GEF为异面EF与CD所成的角，再在Rt△EFG中，求出此角即可．
点评：本小题主要考查异面直线所成的角，考查空间想象能力、运算能力和推理论证能力，属于基础题．
练习册系列答案
相关题目
15、如图所示，在四面体ABCD中，E，F，G分别是棱AB，AC，CD的中点，则过E，F，G的截面把四面体分成两部分的体积之比VADEFGH：VBCEFGH=在正四面体ABCD中，E，F，G分别为AB，CD，BC的中点，则直线EF与直线AG所成角的余弦值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
（2012•闸北区二模）如图，菱形ABCD中，AB=AC=1，其对角线的交点为O，现将△ADC沿对角线AC向上翻折，使得OD⊥OB．在四面体ABCD中，E在AB上移动，点F在DC上移动，且AE=CF=a（0≤a≤1）．