题目内容
已知数列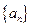 中
中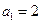 ,
,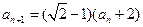 ,
,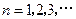 .
.
(Ⅰ)求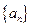 的通项公式;
的通项公式;
(Ⅱ)若数列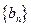 中
中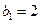 ,
,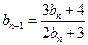 ,
,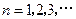 ,
,
证明: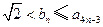 ,
,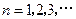 .
.
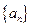 中
中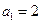 ,
,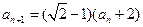 ,
,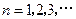 .
.(Ⅰ)求
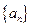 的通项公式;
的通项公式;(Ⅱ)若数列
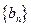 中
中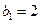 ,
,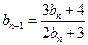 ,
,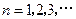 ,
,证明:
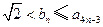 ,
,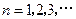 .
.(Ⅰ) 的通项公式为
的通项公式为 ,
,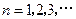 ;(Ⅱ)同解析;
;(Ⅱ)同解析;
 的通项公式为
的通项公式为 ,
,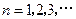 ;(Ⅱ)同解析;
;(Ⅱ)同解析;(Ⅰ)由题设:
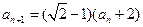

 ,
,
 .
.
所以,数列 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列,
 ,
,
即 的通项公式为
的通项公式为 ,
,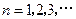 .
.
(Ⅱ)用数学归纳法证明.
(ⅰ)当 时,因
时,因 ,
, ,所以
,所以
 ,结论成立.
,结论成立.
(ⅱ)假设当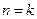 时,结论成立,即
时,结论成立,即 ,
,
也即 .
.
当 时,
时,


 ,
,
又 ,
,
所以


 .
.
也就是说,当 时,结论成立.
时,结论成立.
根据(ⅰ)和(ⅱ)知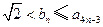 ,
,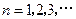 .
.
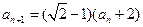

 ,
, .
.所以,数列
 是首项为
是首项为 ,公比为
,公比为 的等比数列,
的等比数列, ,
,即
 的通项公式为
的通项公式为 ,
,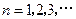 .
.(Ⅱ)用数学归纳法证明.
(ⅰ)当
 时,因
时,因 ,
, ,所以
,所以 ,结论成立.
,结论成立.(ⅱ)假设当
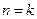 时,结论成立,即
时,结论成立,即 ,
,也即
 .
.当
 时,
时,

 ,
,又
 ,
,所以



 .
.也就是说,当
 时,结论成立.
时,结论成立.根据(ⅰ)和(ⅱ)知
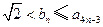 ,
,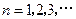 .
.
练习册系列答案
相关题目
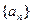 满足
满足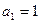 ,点
,点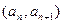 在直线
在直线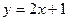 上.
上.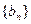 满足
满足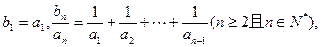
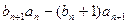 的值;
的值;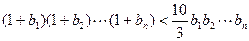
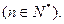
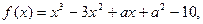 若它是R上的单调函数,且1是它的零点。
若它是R上的单调函数,且1是它的零点。
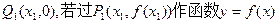 的图象的切线与x轴交于点
的图象的切线与x轴交于点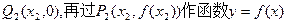 的图象的切线与x轴于
的图象的切线与x轴于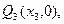 ……,依此下去,过
……,依此下去,过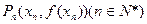 作函数
作函数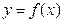 的图象的切线与x轴交于点
的图象的切线与x轴交于点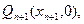 ……,若
……,若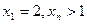 求证:
求证: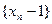 成等比数列;并求数列
成等比数列;并求数列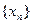 的通项公式
的通项公式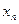 。(已知
。(已知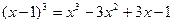 )
) 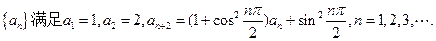
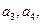 并求数列
并求数列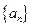 的通项公式;
的通项公式;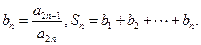 证明:当
证明:当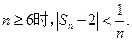
 的各项为正数,前
的各项为正数,前

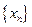 满足
满足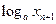 =1+
=1+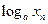 ,且
,且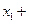
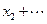
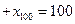 ,则
,则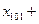
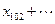 +
+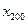 的值为 ( )
的值为 ( )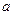
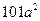
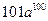
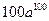
 中,
中, ,
,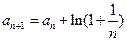 ,则
,则
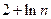



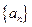 的前n项和为
的前n项和为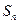 ,若
,若 .
.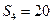 则
则 等于( )
等于( )