题目内容
正项数列 的前n项和为
的前n项和为 ,且
,且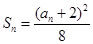 。
。
(Ⅰ)求数列 的通项公式
的通项公式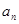 ;
;
(Ⅱ)求证: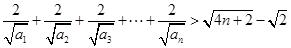 。
。
(Ⅰ)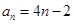 ;(Ⅱ)详见解析.
;(Ⅱ)详见解析.
解析试题分析:(Ⅰ)求数列 的通项公式
的通项公式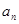 ,由已知
,由已知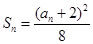 ,这是由
,这是由 求
求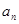 ,可根据
,可根据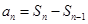 来求,因此当
来求,因此当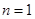 时,
时,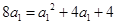 ,解得
,解得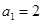 ,当
,当 时,
时, ,整理得
,整理得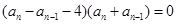 ,从而得数列
,从而得数列 是首项为2,公差为4的等差数列,可写出数列
是首项为2,公差为4的等差数列,可写出数列 的通项公式;(Ⅱ)求证:
的通项公式;(Ⅱ)求证: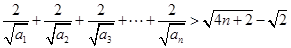 ,由(Ⅰ)可知
,由(Ⅰ)可知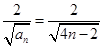 ,观察所证问题,显然需对式子变形,但所证问题的形式为
,观察所证问题,显然需对式子变形,但所证问题的形式为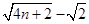 ,这就需要利用放缩法,很容易得证.
,这就需要利用放缩法,很容易得证.
试题解析:(Ⅰ)由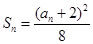 知,当
知,当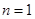 时,
时,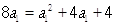 ,解得
,解得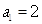 ;
;
当 时,
时,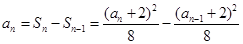 , (3分)
, (3分)
整理得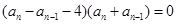 ,又
,又 为正项数列,
为正项数列,
故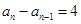 (
( ),因此数列
),因此数列 是首项为2,公差为4的等差数列,
是首项为2,公差为4的等差数列, 。(6分)
。(6分)
(Ⅱ)由于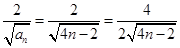
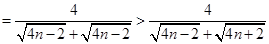
= (8分)
(8分)
因此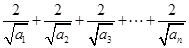
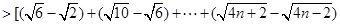
= 。(12分)
。(12分)
考点:求数列的通项公式,放缩法证明不等式.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
公比不为1的等比数列{an}的前n项和为Sn,且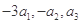 成等差数列,若
成等差数列,若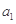 =1,则
=1,则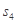 =( ).
=( ).
| A.-20 | B.0 | C.7 | D.40 |
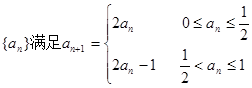 若
若
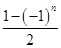 an-
an-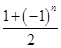 bn,求数列{cn}的前2n项和T2n.
bn,求数列{cn}的前2n项和T2n.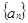 的前
的前 项和
项和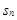 满足
满足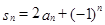 ,
,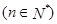
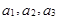
 ,求证:数列
,求证:数列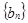 为等比数列,并指出
为等比数列,并指出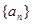 的各项都是1或2.首项为1,且在第
的各项都是1或2.首项为1,且在第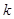 个1和第
个1和第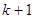 个1之间有
个1之间有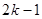 个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前
个2,即1,2,1,2,2,2,1,2,2,2,2,2,1,….记数列的前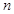 项的和为
项的和为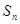 .参考:31×32=992,32×33=1056,44×45=1980,45×46=2070
.参考:31×32=992,32×33=1056,44×45=1980,45×46=2070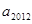 和
和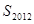 ;
;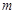 ,使得
,使得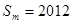 ?如果存在,求出
?如果存在,求出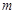 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由. a3,a2成等差数列,则
a3,a2成等差数列,则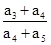 =( ).
=( ).

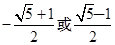
 }中,
}中, =
= =1,
=1, 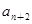 =
=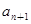 +
+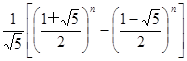 ,根据上述结论,可以知道不超过实数
,根据上述结论,可以知道不超过实数  的最大整数为
的最大整数为