题目内容
等比数列{an}各项均为正数,且a1, a3,a2成等差数列,则
a3,a2成等差数列,则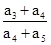 =( ).
=( ).
A.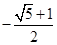 | B. | C.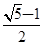 | D.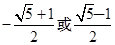 |
C.
解析试题分析:设等比数列{an}的公比为q,因为 ,又a1,
,又a1, a3,a2成等差数列,所以有
a3,a2成等差数列,所以有 ,则
,则 ,所以有
,所以有 ,解得
,解得 ,所以
,所以
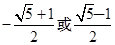 ,又等比数列{an}各项均为正数,所以
,又等比数列{an}各项均为正数,所以
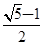 .
.
考点:等比数列的通项公式,等差中项,解一元二次方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知数列 为等差数列,且
为等差数列,且 ,则
,则 的值为 ( )
的值为 ( )
A. | B. | C. | D. |
已知等差数列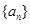 中,
中, ,
, ,则其公差是( )
,则其公差是( )
| A.6 | B.3 | C.2 | D.1 |
已知等差数列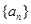 的前
的前 项和为
项和为 ,若
,若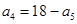 ,则
,则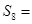 ( )
( )
A.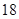 | B. | C. | D.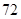 |
设函数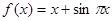 ,则
,则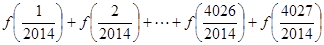 的值为( ).
的值为( ).
A.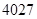 | B.2014 | C.2013 | D.0 |
等差数列 的第15项为( )
的第15项为( )
| A.53 | B.40 | C.63 | D.76 |
在等差数列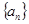 中,
中, ,则
,则 的值为( ).
的值为( ).
| A.27 | B.31 | C.30 | D.15 |
已知等差数列{an}中,|a3|=|a9|,公差d<0,Sn是数列{an}的前n项和,则( )
| A.S5>S6 | B.S5<S6 | C.S6=0 | D.S5=S6 |
 的前n项和为
的前n项和为 ,且
,且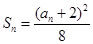 。
。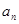 ;
;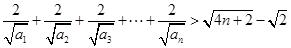 。
。