题目内容
数列 的通项公式是
的通项公式是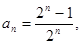 其前
其前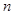 项和为
项和为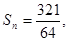 则项数
则项数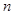 等于
等于
| A.6 | B.9 | C.10 | D.13 |
A
解析试题分析:先将数列的通项变形,再求和,利用已知条件建立方程,即可求得数列的项数n
解:因为 ,所以
,所以
由 得:
得: 。故选A。
。故选A。
考点:数列的求和.
点评:本题考查了数列的通项,考查数列的求和,解题时掌握公式是关键,属于基础题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
阅读如图程序框图,若输入的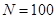 ,则输出的结果是( )
,则输出的结果是( )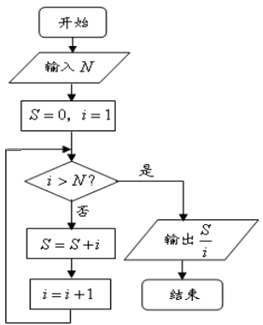
A.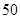 | B.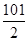 | C.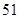 | D.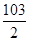 |
数列 的通项公式
的通项公式 ,则该数列的前( )项之和等于
,则该数列的前( )项之和等于 .
.
A. | B. | C. | D. |
设 ( )
( )
| A.4 | B.5 | C.6 | D.10 |
设数列{an}.
A.若 =4n,n∈N*,则{an}为等比数列 =4n,n∈N*,则{an}为等比数列 |
B.若anan+2= ,n∈N*,则{an}为等比数列 ,n∈N*,则{an}为等比数列 |
| C.若aman=2m+n,m,n∈N*,则{an}为等比数列 |
| D.若anan+3=an+1an+2,n∈N*,则{an}为等比数列 |
数列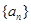 的通项公式
的通项公式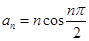 ,其前
,其前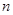 项和为
项和为 ,则
,则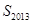 等于( )
等于( )
| A.1006 | B.2012 | C.503 | D.0 |
已知数列{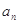 }满足
}满足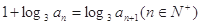 ,且
,且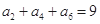 ,则
,则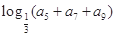 的值是 ( )
的值是 ( )
A.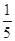 | B.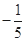 | C.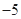 | D.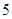 |
若数列{cn}的通项cn=(2n-1)·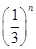 ,则数列{cn}的前n项和Rn=( )
,则数列{cn}的前n项和Rn=( )
A.1-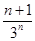 | B.1-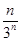 | C.1+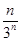 | D.1+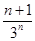 |
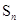 为数列
为数列 的前
的前 项和,且
项和,且 ,数列
,数列 满足
满足 ,数列
,数列 满足
满足 .
. .
.