题目内容
已知数列{an}中,a1=![]() ,a2=
,a2=![]() ,且数列{bn}是公差为-1的等差数列,其中bn=log2(an+1-
,且数列{bn}是公差为-1的等差数列,其中bn=log2(an+1-![]() ),数列{cn}是公比为
),数列{cn}是公比为![]() 的等比数列,其中cn=an+1-
的等比数列,其中cn=an+1-![]() ,求数列{an}的通项公式及它的前n项和.
,求数列{an}的通项公式及它的前n项和.
∵a1=![]() ,a2=
,a2=![]() ,
,
∴b1=log2(![]() -
-![]() ×
×![]() )=-2,c1=
)=-2,c1=![]() -
-![]() ×
×![]() =
=![]() .
.
∵{bn}是公差为-1的等差数列,{cn}是公比为![]() 的等比数列.
的等比数列.
∴bn=
即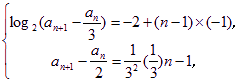 即
即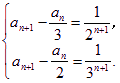
消去an+1,得an=![]() -
-![]() .
.
Sn=a1+a2+…+an=3(![]() +
+![]() +
+![]() +…+
+…+![]() )+2(
)+2(![]() +
+![]() +
+![]() +…+
+…+![]() )
)
=3×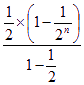 2×
2×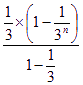 =3-
=3-![]() -1+
-1+![]() .
.
解析:
求通项公式就是求一个关于n的未知函数.在事先无法估计函数的形式结构时,只要列出关于这个未知函数的方程或方程组即可求解.这正是数学思维的基本观点之一——方程观点在求函数解析式问题中的应用.
an是关于n的未知函数.由已知条件,事先无法估计an的解析式的形式结构,因此不能用待定系数法求an.但是利用等差数列{bn}和等比数列{an}可以列出关于an+1和an的两个等式,视它们为关于an+1和an的方程组,消去an+1即可得an.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
已知数列{an}中,a1=1,2nan+1=(n+1)an,则数列{an}的通项公式为( )
A、
| ||
B、
| ||
C、
| ||
D、
|