题目内容
如图,△OAB是边长为2的正三角形.直线x = t截这个三角形所得的,位于此直线左方的图形的面积为y.求函数y = f ( x )的解析式,并求出其定义域和值域.
答案:
解析:
提示:
解析:
| 解:如图, ∵ | OA | = | OB |
= | AB | = 2,
∴ 点B在OA上的射影D点的坐标为(1,0). 当 0 < t ≤1时,所截图形是一个直角三角形, ∴ 当 1< t < 2时,所截图形是一个四边形,它的面积可由正三角形OAB的面积减去一个直角三角形的面积来计算,即:
于是有 此函数的定义域为 由于当 0 < t ≤1 时, 当 1< t < 2时, ∴ 所求值域为 |
提示:
| 如图,由于直线x = t的位置不同,所截得图形的形状也不同,当直线x = t位于直线BD(D是B在OA上射影)左方时,截得图形是直角三角形,而位于右方时,截得图形为四边形.因此应对直线x = t可能允许的位置作出分类讨论. |

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目

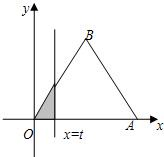 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象.
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).试求函数f(t)的解析式,并画出函数y=f(t)的图象. 如图,△OAB是边长为1的等边三角形,直线x=t截这个三角形位于此直线左方的图形面积(图中阴影部分)为y,求函数y=f(t)的解析式.
如图,△OAB是边长为1的等边三角形,直线x=t截这个三角形位于此直线左方的图形面积(图中阴影部分)为y,求函数y=f(t)的解析式. 如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t).
如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(t>0)左侧的图形的面积为f(t). 如图,△OAB是边长为4的正三角形,记△OAB位于直线x=t(0<t<6)左侧的图形的面积为f(t),试求f(t)的解析式.
如图,△OAB是边长为4的正三角形,记△OAB位于直线x=t(0<t<6)左侧的图形的面积为f(t),试求f(t)的解析式. (2010•武汉模拟)如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积f(t),则函数f(t)的解析式为:
(2010•武汉模拟)如图,△OAB是边长为2的正三角形,记△OAB位于直线x=t(0<t≤2)左侧的图形的面积f(t),则函数f(t)的解析式为: