题目内容
(本题满分13分)已知数列{a![]() }对任意的n∈N,n≥2时有a
}对任意的n∈N,n≥2时有a![]() =3a
=3a![]() +2,S
+2,S![]() =18.(1)计算a
=18.(1)计算a![]() 、a
、a![]() 、a
、a![]() 、a
、a![]() 、a
、a![]() 的值;(2)若数列{T
的值;(2)若数列{T![]() }有T
}有T![]() =an+1-a
=an+1-a![]() ,求T
,求T![]() 的表达式;(3)求数列{a
的表达式;(3)求数列{a![]() }的通项公式.
}的通项公式.
(Ⅰ) a![]() =4,a
=4,a![]() =14 ,a
=14 ,a![]() =44,a
=44,a![]() =134,a
=134,a![]() =404. (Ⅱ) T
=404. (Ⅱ) T![]() =10·3
=10·3![]() .(Ⅲ)a
.(Ⅲ)a![]() =5·3
=5·3![]() -1.
-1.
解析:
:(1)当n=2,3,4,5时,由a![]() =3a
=3a![]() +2,S
+2,S![]() =a
=a![]() +a
+a![]() =18求得:a
=18求得:a![]() =4,a
=4,a![]() =14,易得,a
=14,易得,a![]() =44,a
=44,a![]() =134,a
=134,a![]() =404.
=404.
(2)由a![]() =3a
=3a![]() +2,
+2,![]() ;
;
由T![]() =a
=a![]() -a
-a![]() ,得到T
,得到T![]() =a
=a![]() -a
-a![]() =10.即数列{T
=10.即数列{T![]() }是以10为首项,3为公比的等比数列.即得,T
}是以10为首项,3为公比的等比数列.即得,T![]() =10·3
=10·3![]() .
.
(3)由已知a![]() =3a
=3a![]() +2和T
+2和T![]() =a
=a![]() -a
-a![]() =10·3
=10·3![]() ,得方程组:
,得方程组:![]() 解得,a
解得,a![]() =5·3
=5·3![]() -1.
-1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
. 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由.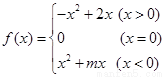 为奇函数;
为奇函数; 以及m的值;
以及m的值; 的图象;
的图象;
 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线
 取得最小值时点P的坐标.
取得最小值时点P的坐标.  是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆 于
于 两点
两点 ,求直线
,求直线 的方程;
的方程; 恒过一定点.
恒过一定点.