题目内容
(本题满分13分)已知圆C:
(1)若平面上有两点A(1 , 0),B(-1 , 0),点P是圆C上的动点,求使 取得最小值时点P的坐标.
取得最小值时点P的坐标.
(2) 若 是
是 轴上的动点,
轴上的动点, 分别切圆
分别切圆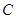 于
于 两点
两点
①若 ,求直线
,求直线 的方程;
的方程;
②求证:直线 恒过一定点.
恒过一定点.
【答案】
解:(1)设P(x , y), 则由两点之间的距离公式知
 =
= =2
=2
要使 取得最小值只要使
取得最小值只要使 最小即可
最小即可
又P为圆上的点,所以 =
= (
( 为半径)
为半径)
∴ 此时直线
此时直线
由 解得
解得 或
或 (舍去)∴点P的坐标为
(舍去)∴点P的坐标为
…………4分
(2) ①设 因为圆
因为圆 的半径
的半径 , 而
, 而 则
则 ,
,
 而
而 为等边三角形。
为等边三角形。
 即
即
所求直线 的方程:
的方程: …………………8分
…………………8分
②
 则
则 是以
是以 为直径的圆上。设
为直径的圆上。设 则
则
以 为直径的圆
为直径的圆 的方程:
的方程: 即
即
 与圆
与圆 :
: 联立,消去
联立,消去 得
得 ,故无论取
,故无论取 何值时,直线
何值时,直线 恒过一定点
恒过一定点 .13分
.13分
【解析】略

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 的两个顶点
的两个顶点 的坐标分别是
的坐标分别是 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
. 的轨迹
的轨迹 的方程,并判断轨迹
的方程,并判断轨迹 时,过点
时,过点 的直线
的直线 交曲线
交曲线 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 (
( 不重合) 试问:直线
不重合) 试问:直线 与
与 轴的交点是否是定点?若是,求出定点,若不是,请说明理由.
轴的交点是否是定点?若是,求出定点,若不是,请说明理由. 为奇函数;
为奇函数;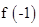 以及m的值;
以及m的值; 的图象;
的图象;
 有三个零点,求实数k的取值范围.
有三个零点,求实数k的取值范围.
 的图象上横坐标为
的图象上横坐标为 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值; 的图象与函数
的图象与函数 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线