题目内容
（1）已知数列{an}，a1=1，以后各项由an=an-1+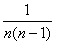
（n≥2）给出，求出数列{an}的通项公式；
（2）已知数列{an}，a1=2，an+1=2an，求数列{an}的通项公式。
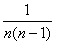（n≥2）给出，求出数列{an}的通项公式； （2）已知数列{an}，a1=2，an+1=2an，求数列{an}的通项公式。
解：（1）由an=an-1+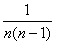得an-an-1=
，
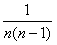∴an=（an-an-1）+（an-1-an-2）+... +（a3-a2）+（a2-a1）+a1
；
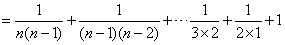
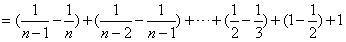
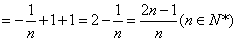（2）由a1=2，an+1=2an得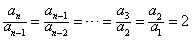
，
∴
。
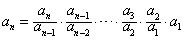
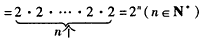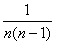得an-an-1=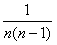，∴an=（an-an-1）+（an-1-an-2）+... +（a3-a2）+（a2-a1）+a1
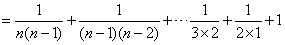
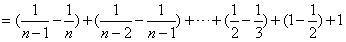
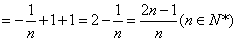；（2）由a1=2，an+1=2an得
，∴
。
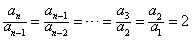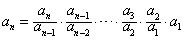
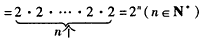练习册系列答案
相关题目
（1）已知数列{an}的第1项 a1=1，且an+1=
（ n=1，2，3…）使用归纳法归纳出这个数列的通项公式．（不需证明）
（2）用分析法证明：若a＞0，则
-
≥a+
-2．
| an |
| 1+an |
（2）用分析法证明：若a＞0，则
a2+
|
| 2 |
| 1 |
| a |