题目内容
【题目】已知数列![]() 满足:对任意
满足:对任意![]() ,若
,若![]() ,则
,则![]() ,且
,且![]() ,设
,设![]() ,集合
,集合![]() 中元素的最小值记为
中元素的最小值记为![]() ;集合
;集合![]() ,集合
,集合![]() 中元素最小值记为
中元素最小值记为![]() .
.
(1)对于数列:![]() ,求
,求![]() ,
,![]() ;
;
(2)求证:![]() ;
;
(3)求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)证明见解析;(3)416
(2)证明见解析;(3)416
【解析】
(1)根据题目,直接代入求解即可.
(2)利用反正法进行证明即可.
(3)欲使![]() 尽可能大,则任意连续三项和要尽量整体控制大,然后,分类讨论即可进行求解
尽可能大,则任意连续三项和要尽量整体控制大,然后,分类讨论即可进行求解
(1)![]()
(2)若![]() ,记
,记![]()
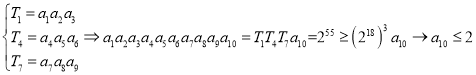
则![]() ,同样操作
,同样操作![]() 这三组数据得到
这三组数据得到![]() ,这与
,这与![]() ,
,![]() 矛盾,则
矛盾,则
![]() ,构造数列:
,构造数列:![]()
(3)欲使![]() 尽可能大,则任意连续三项和要尽量整体控制大,
尽可能大,则任意连续三项和要尽量整体控制大,![]() 如果放在数列中前
如果放在数列中前
后各有2个数,则![]() 这里对应含有
这里对应含有![]() 项的3个连续和,这3个和值显然均大于
项的3个连续和,这3个和值显然均大于![]() ,
,
同理也去控制![]() 项有
项有![]() ,这3个和值显然均大于
,这3个和值显然均大于![]() ,如果我们保证这6项不重叠,
,如果我们保证这6项不重叠,
则8个和,就先处理了6个,剩下2个要使得最小值最大,就有如图排列这种排列:
![]() ,则
,则![]()
考虑![]() 其中
其中![]() ,这一组的和记
,这一组的和记
![]()
可以很快得到![]()
记![]() ,若
,若![]() ,则
,则![]() 这8个数字都要大于等于448,
这8个数字都要大于等于448,
![]() 至多各对应3个数字,
至多各对应3个数字,![]() 对应一个数字,那么这样最多只有7个数字大于等于448,矛盾
对应一个数字,那么这样最多只有7个数字大于等于448,矛盾
构造数列:![]() ,则
,则![]() .
.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目