题目内容
（本小题满分12分）
在直角坐标系中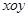
中，曲线C1的参数方程为
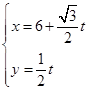（t为参数）；在以O为极点，x轴的正半轴为极轴的极坐标系中，曲线C2的极坐标方程为
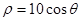，曲线C1与C2交于A、B两点，求|AB|.
在直角坐标系中
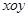中，曲线C1的参数方程为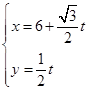（t为参数）；在以O为极点，x轴的正半轴为极轴的极坐标系中，曲线C2的极坐标方程为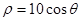，曲线C1与C2交于A、B两点，求|AB|.|AB|＝|t2－t1|＝
＝3．
＝3．本试题主要是考查了极坐标和直角坐标的互换，以及参数方程的综合运用。
由于在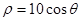的两边同乘以
，得
，可以得到曲线C2的直角坐标方程为x2＋y2＝10x，曲线C1的参数方程为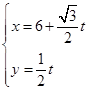代入到上述方程中得到关于t的方程，求解得到结论。
解：在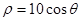的两边同乘以，得
则曲线C2的直角坐标方程为x2＋y2＝10x，……………………………………3分
将曲线C1的参数方程代入上式，得(6＋t)2＋t2＝10(6＋t)，
整理，得t2＋t－24＝0，
设这个方程的两根为t1，t2，则t1＋t2＝－，t1t2＝－24，
所以|AB|＝|t2－t1|＝＝3．………………………12分
由于在
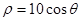的两边同乘以，得，可以得到曲线C2的直角坐标方程为x2＋y2＝10x，曲线C1的参数方程为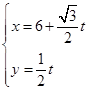代入到上述方程中得到关于t的方程，求解得到结论。解：在
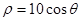的两边同乘以，得则曲线C2的直角坐标方程为x2＋y2＝10x，……………………………………3分
将曲线C1的参数方程代入上式，得(6＋t)2＋t2＝10(6＋t)，
整理，得t2＋t－24＝0，
设这个方程的两根为t1，t2，则t1＋t2＝－，t1t2＝－24，
所以|AB|＝|t2－t1|＝
＝3．………………………12分
练习册系列答案
相关题目
到圆
的圆心的距离为（ ）
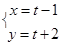（t为参数）的曲线与坐标轴的交点坐标为（ ）
的极坐标方程是
，以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线
的参数方程是
（
为参数）若直线
（
为参数），则它的斜截式方程为 。
被双曲线
截得的弦长为__________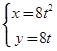
（t为参数），若斜率为1的直线经过抛物线C的焦点，且与圆
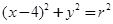（r＞0）相切，则r＝ 
化为以
为参数的参数方程可以是（ ）
