题目内容
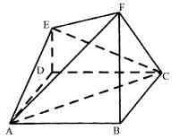
已知ABCD是边长为4的正方形, E、F分别是AB、AD中点, GC垂直于ABCD所在平面且GC=2, 点B到平面EFG的距离的平方为_________.
答案:4/11
解析:
提示:
解析:
|
解: 连结BD, AC. 设交点为O. EF∩AC=H ∵ BD∥EF, ∴B到平面GEF的距离可以转化成O到平面GEF之距离. 连结GH, 过O作OM⊥GH且交GH于M. ∵ EF⊥AC, GC⊥平面AC则GC⊥EF. ∴ EF⊥平面GHC. ∴ EF⊥OM OM⊥GH 则OM⊥平面GEF. △OMH相似于△GCH.
∵ GC=2 GH=
∴ OM=
|
提示:
|
该题难度较大. 连结BD, 设BD的中点为O, 可以将所求的距离转化为O到平面GEF的距离. 设EF∩AC=H. 连结GH, 只要作OM⊥GH, 垂足为M, OM即为所求. |

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 . OM
. OM
 如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.
如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2. 如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.
如图,已知ABCD是边长为a的正方形,E,F分别是AB,AD的中点,CG⊥面ABCD,CG=a.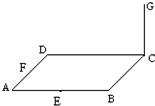 已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离.
已知ABCD是边长为4的正方形,E、F分别是AB、AD的中点,GC垂直于ABCD所在的平面,且GC=2.求点B到平面EFG的距离. 如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.
如图,已知ABCD是边长为2的正方形,DE⊥平面ABCD,BF⊥平面ABCD,且FB=2DE=2.