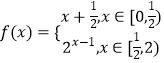题目内容
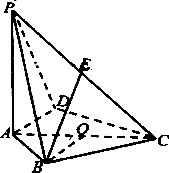
【题目】如图,已知四棱锥S﹣ABCD,SB⊥AD,侧面SAD是边长为4的等边三角形,底面ABCD为菱形,侧面SAD与底面ABCD所成的二面角为120°.
(1)求点S到平面ABCD的距离;
(2)若E为SC的中点,求二面角A﹣DE﹣C的正弦值.
【答案】
(1)
解:如图,作SO⊥平面ABCD,垂足为点O.
连接OB,OA,OD,OB与AD交于点F,连接SF.
∵SB⊥AD,
∴OB⊥AD.
∵SA=SD,
∴OA=OD.
∴点F为AD的中点,所以SF⊥AD.
由此知∠SFB为侧面SAD与底面ABCD所成的二面角的平面角,
∴∠SFB=120°,
∵侧面SAD是边长为4的等边三角形,
∴SF= ![]() =2
=2 ![]() ,
,
∴SO=SFsin60°=2 ![]() =3,
=3,
即点S到平面ABCD的距离为3
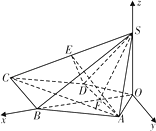
(2)
解:如图以O为坐标原点,使y轴与BC平行,OB,OS所在直线分别为y轴、z轴建立空间直角坐标系,
由已知得:A( ![]() ,2,0),D(
,2,0),D( ![]() ,0),C(3
,0),C(3 ![]() ,﹣4,0),E(
,﹣4,0),E( ![]() ,﹣2,
,﹣2, ![]() ),
),
![]() =(0,﹣4,0),
=(0,﹣4,0), ![]() =(
=( ![]() ,0,
,0, ![]() ),
), ![]() =(﹣
=(﹣ ![]() ,2,
,2, ![]() ),
),
设平面ADE的法向量为 ![]() ,
,
则 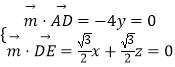 令x=
令x= ![]() ,得
,得 ![]() =(
=( ![]() ,0,﹣1).
,0,﹣1).
设平面DEC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 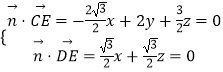 ,令x=
,令x= ![]() ,得
,得 ![]() =(
=( ![]() ,3,﹣1),
,3,﹣1),
设二面角的平面角为θ,
则cosθ= ![]() =
= ![]() =
= ![]() ,
,
∴sinθ= ![]() =
= ![]() ,
,
∴二面角A﹣DE﹣C的正弦值为 ![]()
【解析】(1)解:作SO⊥平面ABCD,连接OB,OA,OD,OB与AD交于点F,连接SF.推导出OB⊥AD,SF⊥AD.从而∠SFB为侧面SAD与底面ABCD所成的二面角的平面角,由此能求出点S到平面ABCD的距离.(2)以O为坐标原点,使y轴与BC平行,OB,OS所在直线分别为y轴、z轴建立空间直角坐标系,利用向量法能求出二面角A﹣DE﹣C的正弦值.

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案