题目内容
(本题满分12分)
如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() 的延长线交
的延长线交![]() 于
于![]() 。现将
。现将![]() 沿
沿![]() 折起,折成二面角
折起,折成二面角![]() ,连接
,连接![]() .
.
(I)求证![]() :平面
:平面![]() 平面
平面![]() ;
;
(II)当![]()
![]() 时,求二面角
时,求二面角![]() 大小的余弦值.
大小的余弦值.
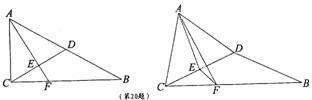
证明:(I)在![]() ,
,
![]() 又E是CD的中点,得AF⊥CD. …………
又E是CD的中点,得AF⊥CD. …………![]() ..3分
..3分
折起后,AE⊥CD,EF⊥![]() CD,又AE∩EF=E
CD,又AE∩EF=E![]() ,AE
,AE![]() 平
平![]() 面AED,EF
面AED,EF![]() 平面AEF,
平面AEF,
故CD⊥平面AEF,又CD![]() 平面CDB,故平面AEF⊥平面CBD. …………5分
平面CDB,故平面AEF⊥平面CBD. …………5分
(II)过点A作AH⊥EF,垂足H落在FE的延长线上.
因为CD⊥平面AEF,所以CD⊥AH,所以AH⊥平面CBD. …………6分
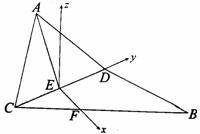
以E为原点,EF所在直线为x轴,ED所在直线为y轴,![]() 过E与AH平行的直线为z轴
过E与AH平行的直线为z轴
建立如图空间直角坐标系. …..……………………7分
|
由(I)可知∠AEF即为所求二面角的平面角,设为![]() ,并设AC=
,并设AC= ![]() ,可得
,可得
![]() …………8分
…………8分
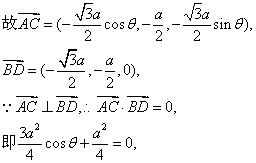
得![]()
![]() …………11分
…………11分
故二面角A—CD—B大小的余弦值为![]() …………12分
…………12分

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 <1,xÎR }.
<1,xÎR }. ,求实数a的取值范围.
,求实数a的取值范围. (
( ,
, 为常数),且方程
为常数),且方程 有两个实根为
有两个实根为 .
. 的解析式;
的解析式; 中,四边形
中,四边形 是边长为
是边长为 的正方形,
的正方形, ,
, 为
为 上的点,且
上的点,且 ⊥平面
⊥平面
 ⊥平面
⊥平面
 的大小;
的大小; 到平面
到平面