题目内容
已知函数f(x)=x2-2alnx,(a>0),令g(x)=f(x)-2ax,若g(x)有两个零点,则a的取值范围是
- A.
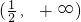
- B.

- C.
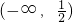
- D.

A
分析:g(x)有两个零点,x2-2ax=2alnx两侧的图象有两个交点,即y1=x2-2ax,y2=2alnx有两个交点,二次函数的对称轴是x=a且过原点,对数型函数若递减时,不能有两个交点,且对称轴越大,有两个交点.
解答:∵函数f(x)=x2-2alnx,(a>0),
令g(x)=f(x)-2ax=x2-2ax-2alnx=0,
∵g(x)有两个零点
∴x2-2ax=2alnx两侧的图象有两个交点,
即y1=x2-2ax,y2=2alnx有两个交点,
二次函数的对称轴是x=a,过原点,
当对数型函数所过的与横轴的交点在二次函数与横轴交点的左边,
即1<2a,
所以a>
且对称轴越大,有两个交点,
故选A.
点评:本题考查函数的零点,在解题时注意对于两个函数的整理,变化成基本初等函数,可以根据选择题目的特殊性来解,即取值检验.
分析:g(x)有两个零点,x2-2ax=2alnx两侧的图象有两个交点,即y1=x2-2ax,y2=2alnx有两个交点,二次函数的对称轴是x=a且过原点,对数型函数若递减时,不能有两个交点,且对称轴越大,有两个交点.
解答:∵函数f(x)=x2-2alnx,(a>0),
令g(x)=f(x)-2ax=x2-2ax-2alnx=0,
∵g(x)有两个零点
∴x2-2ax=2alnx两侧的图象有两个交点,
即y1=x2-2ax,y2=2alnx有两个交点,
二次函数的对称轴是x=a,过原点,
当对数型函数所过的与横轴的交点在二次函数与横轴交点的左边,
即1<2a,
所以a>

且对称轴越大,有两个交点,
故选A.
点评:本题考查函数的零点,在解题时注意对于两个函数的整理,变化成基本初等函数,可以根据选择题目的特殊性来解,即取值检验.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|