题目内容
设函数f(x)=(x+1)2-2klnx.
(1)当k=1时,求函数f(x) 在点P(1,4)处的切线方程
(2)当k<0时,求函数g(x)=f'(x)在区间(0,2]上的最小值.
解:(1)k=1,f(x)=(x+1)2-2lnx.
则f′(x)=2x+2- .
.
∵k=f′(1)=2+2-2=2,
∴函数f(x) 在点P(1,4)处的切线方程为:
y-4=2(x-1),
整理得2x-y+2=0.
(2)当k<0时,g(x)=f′(x)=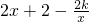 .
.
g(x)=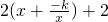 ≥
≥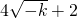 ,
,
当且仅当x=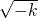 时,上述“≥”中取“=”.
时,上述“≥”中取“=”.
①若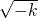 ∈(0,2],即当k∈[-4,0)时,
∈(0,2],即当k∈[-4,0)时,
函数g(x)在区间(0,2]上的最小值为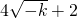 ;
;
②若k<-4,则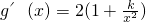 在(0,2]上为负恒成立,
在(0,2]上为负恒成立,
故g(x)在区间(0,2]上为减函数,
于是g(x)在区间(0,2]上的最小值为g(2)=6-k.
综上所述,当k∈[-4,0)时,
函数g(x)在区间(0,2]上的最小值为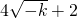 ;
;
当k<-4时,函数g(x)在区间(0,2]上的最小值为6-k.
分析:(1)k=1,f(x)=(x+1)2-2lnx.则f′(x)=2x+2- .切线的斜率k=f′(1)=2+2-2=2,由此能求出函数f(x) 在点P(1,4)处的切线方程.
.切线的斜率k=f′(1)=2+2-2=2,由此能求出函数f(x) 在点P(1,4)处的切线方程.
(2)因为g(x)=f'(x),分区间讨论k的取值并根据a+b≥2 当且仅当a=b时取等号的方法求出最小值即可.
当且仅当a=b时取等号的方法求出最小值即可.
点评:考查学生利用导数研究函数单调性的能力,利用导数求闭区间上函数最值的能力,a+b≥2 当且仅当a=b时取等号的灵活运用.本题有一定的探索性.综合性强,难度大,易出错.
当且仅当a=b时取等号的灵活运用.本题有一定的探索性.综合性强,难度大,易出错.
则f′(x)=2x+2-
 .
.∵k=f′(1)=2+2-2=2,
∴函数f(x) 在点P(1,4)处的切线方程为:
y-4=2(x-1),
整理得2x-y+2=0.
(2)当k<0时,g(x)=f′(x)=
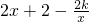 .
.g(x)=
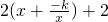 ≥
≥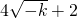 ,
,当且仅当x=
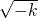 时,上述“≥”中取“=”.
时,上述“≥”中取“=”.①若
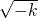 ∈(0,2],即当k∈[-4,0)时,
∈(0,2],即当k∈[-4,0)时,函数g(x)在区间(0,2]上的最小值为
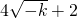 ;
;②若k<-4,则
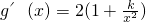 在(0,2]上为负恒成立,
在(0,2]上为负恒成立,故g(x)在区间(0,2]上为减函数,
于是g(x)在区间(0,2]上的最小值为g(2)=6-k.
综上所述,当k∈[-4,0)时,
函数g(x)在区间(0,2]上的最小值为
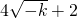 ;
;当k<-4时,函数g(x)在区间(0,2]上的最小值为6-k.
分析:(1)k=1,f(x)=(x+1)2-2lnx.则f′(x)=2x+2-
 .切线的斜率k=f′(1)=2+2-2=2,由此能求出函数f(x) 在点P(1,4)处的切线方程.
.切线的斜率k=f′(1)=2+2-2=2,由此能求出函数f(x) 在点P(1,4)处的切线方程.(2)因为g(x)=f'(x),分区间讨论k的取值并根据a+b≥2
 当且仅当a=b时取等号的方法求出最小值即可.
当且仅当a=b时取等号的方法求出最小值即可.点评:考查学生利用导数研究函数单调性的能力,利用导数求闭区间上函数最值的能力,a+b≥2
 当且仅当a=b时取等号的灵活运用.本题有一定的探索性.综合性强,难度大,易出错.
当且仅当a=b时取等号的灵活运用.本题有一定的探索性.综合性强,难度大,易出错. 
练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
 的最小值;
的最小值; 的最小值;
的最小值;