题目内容
（16分）已知数列
是等差数列，
（1）判断数列
是否是等差数列，并说明理由；
（2）如果
，试写出数列的通项公式；
（3）在（2）的条件下，若数列得前n项和为
，问是否存在这样的实数
，使当且仅当
时取得最大值。若存在，求出的取值范围；若不存在，说明理由。
【答案】
（1）数列
是以
为公差的等差数列
（2）
（3）
【解析】（1）设
的公差为
，则
数列是以为公差的等差数列…………4分
（2）
两式相减：
…………6分
…………8分
…………10分
（3）因为当且仅当
时
最大
…………12分
即
…………15分
练习册系列答案
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
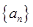是等差数列，若
,
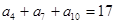，且
,则
_________．
是等差数列，
，则首项
．
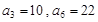是等差数列,
，数列
的前n项和是
，且
.
是等差数列，数列
是等比数列，则
的值为 .
}是等差数列，且满足：a1＋a2＋a3＝6，a5＝5；
}满足：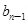
＝
（n≥2，n∈N﹡），b1＝1．
＝
（n∈N﹡），若{
，求