题目内容
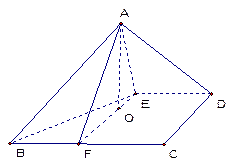
ABCD为平行四边形,P为平面ABCD外一点,PA⊥面ABCD,且PA=AD=2,AB=1,AC=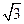 。
。

求证:平面ACD⊥平面PAC;
求异面直线PC与BD所成角的余弦值;
设二面角A—PC—B的大小为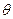 ,试求
,试求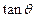 的值。
的值。
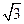 。
。
求证:平面ACD⊥平面PAC;
求异面直线PC与BD所成角的余弦值;
设二面角A—PC—B的大小为
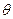 ,试求
,试求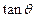 的值。
的值。(1) 略
(2)

(3)

(1)略;(2) ;
;
(3)过A作AE⊥PC交PC于E,过E作EF⊥PC交PB于F,连结AE。则二面角A—PC—B的平面角为∠AEF即∠AEF=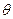 。
。
在Rt⊿APC中,PC= ,
, ,
,
在⊿PBC中,PB= ,BC=2,
,BC=2, ,
,
在Rt⊿PEF中,
在⊿PAF中,PF= ,
,
在⊿AEF中,
 ;
;(3)过A作AE⊥PC交PC于E,过E作EF⊥PC交PB于F,连结AE。则二面角A—PC—B的平面角为∠AEF即∠AEF=
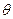 。
。在Rt⊿APC中,PC=
 ,
, ,
,在⊿PBC中,PB=
 ,BC=2,
,BC=2, ,
,在Rt⊿PEF中,

在⊿PAF中,PF=
 ,
,在⊿AEF中,


练习册系列答案
相关题目

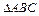 中,
中,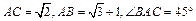 ,
,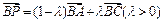 ,
,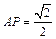 .
.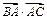 的值;
的值;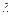 的值;
的值; AQ与BP交于点M,
AQ与BP交于点M,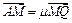 ,求实数
,求实数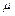 的值.
的值.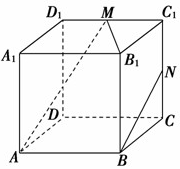
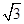 ,侧棱与底面所成角为600,则棱锥的体积为( )
,侧棱与底面所成角为600,则棱锥的体积为( )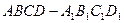 中,底面
中,底面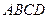 是
是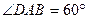 的菱形,
的菱形,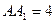 ,
,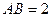 ,点
,点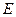 在棱
在棱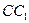 上,点
上,点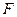 是棱
是棱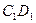 的中点.
的中点.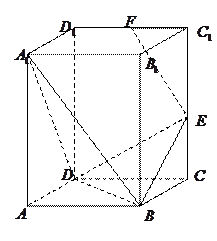
 ;
;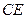 的长度,使得
的长度,使得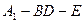 为直二面角.
为直二面角.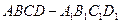 中,棱长为
中,棱长为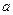
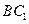 与
与 所成的角;
所成的角;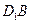 与平面
与平面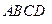 所成角的正切值;
所成角的正切值;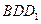
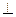 平面
平面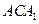 .
. AB-C2为60o,
AB-C2为60o, 则点C
则点C 1与C2之间的距离可能是___________.(写出二个可能值即可)
1与C2之间的距离可能是___________.(写出二个可能值即可)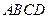 中,
中,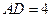 ,
,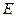 、
、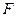 分别是
分别是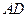 、
、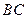 的中点,点
的中点,点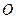 在
在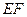 上,且
上,且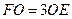 ,把
,把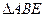 沿着
沿着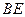 翻折,使点
翻折,使点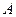 在平面
在平面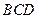 上的射影恰为点
上的射影恰为点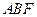
 平面
平面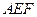 ;
;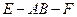 的大小.
的大小.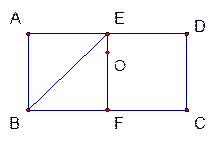
 的等边三角形,另外两个面是等腰直角三角形,则这个三棱锥的体积为
的等边三角形,另外两个面是等腰直角三角形,则这个三棱锥的体积为