题目内容
已知在函数f（x）
图象上，相邻的一个最大值点与一个最小值点恰好在圆x2+y2=R2上，则f（x）的最小正周期为
- A.1
- B.2
- C.3
- D.4
D
分析：先用R表示出周期，得到最大值点和最小值点的坐标后，代入到圆的方程可求出R的值，最后可得答案．
解答：∵x2+y2=R2，∴x∈[-R，R]．
∵函数f（x）的最小正周期为2R，
∴最大值点为（
），相邻的最小值点为（
），
代入圆方程，得R=2，∴T=4．
故选D．
点评：本题主要考查三角函数的性质--周期性．属基础题．三角函数两相邻的最大值与最小值正好等于半个周期．
分析：先用R表示出周期，得到最大值点和最小值点的坐标后，代入到圆的方程可求出R的值，最后可得答案．
解答：∵x2+y2=R2，∴x∈[-R，R]．
∵函数f（x）的最小正周期为2R，
∴最大值点为（
），相邻的最小值点为（），代入圆方程，得R=2，∴T=4．
故选D．
点评：本题主要考查三角函数的性质--周期性．属基础题．三角函数两相邻的最大值与最小值正好等于半个周期．
练习册系列答案
相关题目
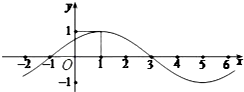（2012•东城区二模）已知函数f（x）=Asin（ωx+φ）（其中x∈R，A＞0，ω＞0，-
已知函数f（x）=Asin（ωx+φ）（其中x∈R，A＞0，ω＞0，-
＜φ＜
）的部分图象如图所示．
已知函数f（x）=Asin（ωx+φ）（其中x∈R，A＞0，ω＞0，-
＜φ＜
）的部分图象如图所示．
已知函数f（x）=Asin（ωx+φ）（其中x∈R，A＞0，ω＞0，-
＜φ＜
）的部分图象如图所示．
已知函数f（x）=Asin（ωx+φ）（其中x∈R，A＞0，ω＞0，-
＜φ＜
）的部分图象如图所示．