题目内容
(16分) 已知函数![]() 的定义域为
的定义域为![]() ,且同时满足:对任意
,且同时满足:对任意![]() ,总有
,总有![]() ,
,![]() ;
;
若![]() ,
,![]() 且
且![]() ,则有
,则有![]() .
.
(1)求![]() 的值;
的值;
(2)试求![]() 的最大值;
的最大值;
(3)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,
,
求证:![]() .
.
1)令![]() ,则
,则![]() ,又由题意,有
,又由题意,有![]()
![]() …………………3分
…………………3分
(2)任取 且![]() ,则0<
,则0<![]()
![]()
![]()
故函数![]() 在
在![]() 上是单调增函数…………6分
上是单调增函数…………6分
![]() 的最大值为
的最大值为![]() ………8分
………8分
(3)由![]()
![]()
又由![]()
![]()
![]() 数列
数列![]() 为首项为1,公比为
为首项为1,公比为![]() 的等比数列,
的等比数列, ![]() ………10分
………10分
当![]() 时,
时,![]() ,不等式成立,
,不等式成立,
当![]() 时,
时,![]()
![]() ,
, ![]()
![]() 不等式成立
不等式成立
假设![]() 时,不等式成立 即
时,不等式成立 即 ![]()
则当![]() 时
时 ![]()
![]()
![]()
![]()
![]()
即 ![]() 时,不等式成立故 对
时,不等式成立故 对![]() ,原不等式成立。…16分
,原不等式成立。…16分

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
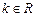 ,函数
,函数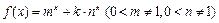 .
.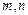 满足
满足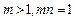 ,函数
,函数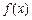 是否具有奇偶性?如果有,求出相应的
是否具有奇偶性?如果有,求出相应的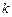
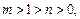 判断函数
判断函数 ,
,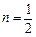 ,且
,且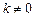 ,求函数
,求函数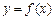 的对称轴或对称中心.
的对称轴或对称中心.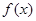 满足满足
满足满足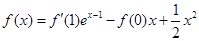 ;
;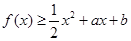 ,求
,求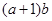 的最大值.
的最大值.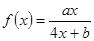
 ,在
,在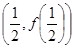 处的
处的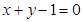 .
. 的解析式;
的解析式;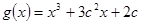
 ,若对任意
,若对任意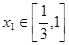 ,总存在
,总存在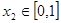 ,使得
,使得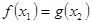 成立,求实数
成立,求实数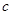 的取值范围.
的取值范围.