题目内容
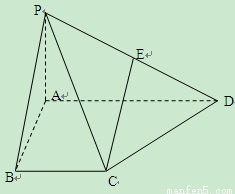
(本题满分12分)如图,已知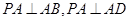 , 四边形
, 四边形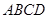 是梯形,
是梯形,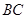 ∥
∥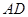 ,
, 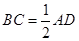 ,
,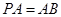 ,
, 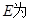
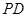 中点。
中点。
(1)求证: ∥ 平面
∥ 平面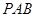 ;
;
(2)求异面直线 与
与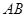 所成角的余弦值。
所成角的余弦值。

【答案】
(1)证明: CE∥面PAB. (6分)
(2)  (12分
(12分
【解析】(1)证明:取PA中点F,连结EF,BF,
∵E为PD中点,∴EF∥AD,且EF= AD,
AD,
又BC∥AD,BC= AD,∴EF∥BC,EF=BC,
AD,∴EF∥BC,EF=BC,
∴四边形BCEF为平行四边形,∴CE∥BF,
∵CE 面PAB, BF
面PAB, BF 面PAB,∴CE∥面PAB. (6分)
面PAB,∴CE∥面PAB. (6分)

(2)由(1)CE∥BF,
∴∠FBA(或其补角)即为CE与AB所成角,
设PA=AB= ,则在Rt
,则在Rt BAF中,AF=
BAF中,AF= ,BF=
,BF= ,∴cosFBA=
,∴cosFBA= ,∴CE与AB所成角的余弦值为
,∴CE与AB所成角的余弦值为 (12分
(12分

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 为底面的直棱柱被平面
为底面的直棱柱被平面 所截而得.
所截而得.  ,
, 为
为 的中点.
的中点.
 时,求平面
时,求平面 为何值时,在棱
为何值时,在棱 上存在点
上存在点 ,使
,使 平面
平面 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱 ,为
,为 中点,
中点, 为
为 中点,
中点, 为
为 上一个动点.
上一个动点.
 ;
; 的平
的平
 中,已知
中,已知 的直径
的直径 的中点.
的中点.
 所成角的正弦值.
所成角的正弦值.
