题目内容
(2012•虹口区二模)已知:曲线C上任意一点到点F(1,0)的距离与到直线x=-1的距离相等.
(1)求曲线C的方程;
(2)如果直线y=k(x-1)交曲线C于A、B两点,是否存在实数k,使得以AB为直径的圆经过原点O?若存在,求出k的值;若不存在,说明理由.
(1)求曲线C的方程;
(2)如果直线y=k(x-1)交曲线C于A、B两点,是否存在实数k,使得以AB为直径的圆经过原点O?若存在,求出k的值;若不存在,说明理由.
分析:(1)利用曲线C上任意一点到点F(1,0)的距离与到直线x=-1的距离相等,可知曲线C的轨迹是以F(1,0)为焦点的抛物线,从而可求曲线C的方程;
(2)将y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0,利用韦达定理,可得x1x2+y1y2=-3≠0,从而可知以AB为直径的圆不经过原点O.
(2)将y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0,利用韦达定理,可得x1x2+y1y2=-3≠0,从而可知以AB为直径的圆不经过原点O.
解答:解:(1)∵曲线C上任意一点到点F(1,0)的距离与到直线x=-1的距离相等.
∴曲线C的轨迹是以F(1,0)为焦点的抛物线
∴曲线C的方程为y2=4x;…(4分)
(2)将y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0…(8分)
记A(x1,y1),B(x2,y2),∴x1x2=1,x1+x2=
,…(10分)
∴y1y2=k2(x1-1)(x2-1)=-4 …(12分)
∴x1x2+y1y2=-3≠0
∴
•
≠0
∴以AB为直径的圆不经过原点O,
∴不存在满足条件的k.…(14分)
∴曲线C的轨迹是以F(1,0)为焦点的抛物线
∴曲线C的方程为y2=4x;…(4分)
(2)将y=k(x-1),代入y2=4x,得k2x2-2(k2+2)x+k2=0…(8分)
记A(x1,y1),B(x2,y2),∴x1x2=1,x1+x2=
| 2(k2+2) |
| k2 |
∴y1y2=k2(x1-1)(x2-1)=-4 …(12分)
∴x1x2+y1y2=-3≠0
∴
| OA |
| OB |
∴以AB为直径的圆不经过原点O,
∴不存在满足条件的k.…(14分)
点评:本题考查轨迹方程的求法,考查向量知识的运用,解题的关键是正确运用抛物线的定义,正确运用韦达定理.

练习册系列答案
相关题目
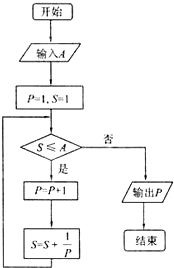 (2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为
(2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为