Question

【题目】根据国家环保部新修订的《 环境空气质量标准》规定：居民区的年平均浓度不得超过微克/立方米，的小时平均浓度不得超过微克/立方米.我市环保局随机抽取了一居民区年天的小时平均浓度（单位：微克/立方米）的监测数据，数据统计如下表：

组别	浓度（微克/立方米）	频数（天）	频率
第一组
第二组
第三组
第四组

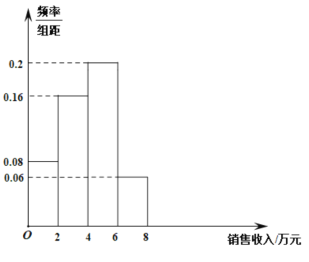
（1）这天的测量结果按上表中分组方法绘制成的样本频率分布直方图如图.

①求图中的值；

②求样本平均数，并根据样本估计总体的思想，从的年平均浓度考虑，判断该居民区的环境质量是否需要改善？并说明理由；

（2）将频率视为概率，对于年的某天，记这天中该居民区的小时平均浓度符合环境空气质量标准的天数为，求的分布列和数学期望.

Answer 1

【答案】（1）①；②需要改进，理由见解析；（2）分布列见解析，.

【解析】

（1）①根据频率分布直方图中所有矩形的面积之和为可求得的值；

②根据频率直方图计算出年该居民区年平均浓度，与作大小比较，由此可得出结论；

（2）由题意可知，进而可得出随机变量的分布列，由此可计算得出随机变量的数学期望值.

（1）①在频率分布直方图中，所有矩形面积之和为，

则，解得；

②年该居民区年平均浓度为（微克/立方米），

因为，所以年该居民区年平均浓度不符合环境空气质量标准，故该居民区的环境需要改进；

（2）由题意，的小时平均浓度符合环境空气质量标准的概率为，

的可能取值为、、、，且，

，，，.

所以，随机变量的分布列如下表所示：

所以，随机变量的数学期望为.