题目内容
已知函数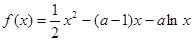 ,
,
(Ⅰ)求函数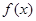 的单调区间;
的单调区间;
(Ⅱ)若函数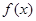 在区间
在区间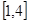 内的最小值为
内的最小值为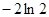 ,求
,求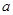 的值.(参考数据
的值.(参考数据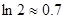 )
)
【答案】
(Ⅰ)详见解析;(Ⅱ)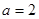 .
.
【解析】
试题分析:(Ⅰ) 本小题首先利用求导的公式与法则求得函数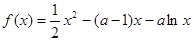 的导数
的导数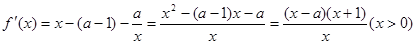 ,通过分析其值的正负可得函数的单调性;
,通过分析其值的正负可得函数的单调性;
(Ⅱ) 本小题主要利用导数分析函数的单调性,根据参数的取值范围得到函数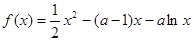 在区间
在区间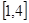 上单调性,然后求得目标函数的最值即可.
上单调性,然后求得目标函数的最值即可.
试题解析:(Ⅰ)由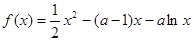 得
得
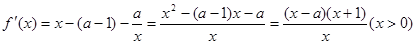 2分
2分
①当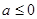 时,
时,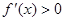 恒成立,
恒成立,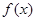 的单调递增区间是
的单调递增区间是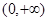 ;
4分
;
4分
②当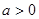 时,
时,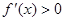
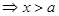 ,
,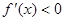
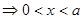 ,
,
可得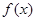 在
在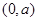 单调递减,
单调递减,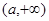 单调递增.
6分
单调递增.
6分
(Ⅱ)结合(Ⅰ)可知:
①当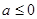 时,
时,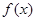 在区间
在区间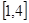 内单调递增,
内单调递增,
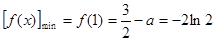
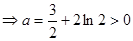 ,
,
与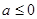 矛盾,舍去;
8分
矛盾,舍去;
8分
②当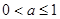 时,
时,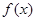 在区间
在区间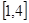 内单调递增,
内单调递增,
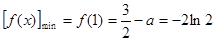
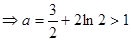 ,
与
,
与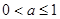 矛盾,舍去; 10分
矛盾,舍去; 10分
③当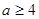 时,
时,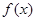 在区间
在区间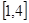 内单调递减,
内单调递减,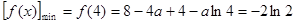 ,
,
得到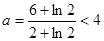 ,舍去;
12分
,舍去;
12分
④当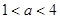 时,
时,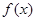 在
在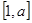 单调递减,
单调递减,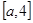 单调递增,
单调递增,
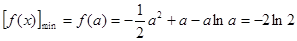 ,
,
令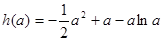 ,则
,则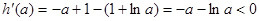 ,故
,故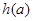 在
在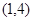 内为减函数,
内为减函数,
又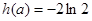 ,
,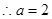 14分
14分
综上得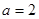 15分
15分
考点:1.求导得公式与法则;2.导数判断单调性.

练习册系列答案
相关题目

 .
. 的单调递增区间;
的单调递增区间; ,函数
,函数 上都有三个零点,求实数
上都有三个零点,求实数 的取值范围.
的取值范围. 分)
分) .
. 的最大值;
的最大值; 中,
中, ,角
,角 满足
满足 ,求
,求