题目内容
已知函数 。
。
(1)求函数 在区间
在区间 上的值域;
上的值域;
(2)是否存在实数a,对任意给定的 ,在区间
,在区间 上都存在两个不同的
上都存在两个不同的 ,使得
,使得 成立。若存在,求出a的取值范围;若不存在,请说明理由。
成立。若存在,求出a的取值范围;若不存在,请说明理由。
解:(1) 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,且
上单调递减,且 的值域为
的值域为
(2)令 ,则由(1)可得
,则由(1)可得 ,原问题等价于:对任意的
,原问题等价于:对任意的
 在
在 上总有两个不同的实根,故
上总有两个不同的实根,故 在
在 不可能是单调函数。
不可能是单调函数。
 ,其中
,其中
① 当 时,
时, 在区间
在区间 上单调递减,不合题意
上单调递减,不合题意
② ②当 时,
时, 在区间
在区间 上单调递增,不合题意
上单调递增,不合题意
③当 ,即
,即 时,
时, 在区间
在区间 上单调递减;
上单调递减; 在区间
在区间 上单调递增,
上单调递增,
由上可得 ,此时必有
,此时必有 且
且
而上 可得
可得 ,则
,则 ,
,
综上,满足条件的a不存在。

练习册系列答案
相关题目
已知过抛物线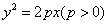 的焦点F的直线交抛物线于
的焦点F的直线交抛物线于 、
、 两点,直线OM、ON(O为坐标原点)分别与准线l相交于P、Q两点,下列命题正确的是 (请填上正确命题的序号)
两点,直线OM、ON(O为坐标原点)分别与准线l相交于P、Q两点,下列命题正确的是 (请填上正确命题的序号)
① ②
② ③
③ =
=
④ ⑤以线段MF为直径的圆必与y轴相切
⑤以线段MF为直径的圆必与y轴相切
一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月产量如表(单位:辆):
| 轿车A | 轿车B | 轿车C | |
| 舒适型 | 100 | 150 | z |
| 标准型 | 300 | 450 | 600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆。
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本。将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率。
 ,c=2+
,c=2+ ,若不等式
,若不等式 成立,则实数a的取值范围是( ).
成立,则实数a的取值范围是( ). } B.{a|
} B.{a| } C.{a|
} C.{a| } D.{a|
} D.{a| }
} 是夹角为
是夹角为 的两个单位向量,则
的两个单位向量,则 模是
模是 (C)
(C) (D)7
(D)7