Question

某工厂要制造A种电子装置41台，B种电子装置66台，需用薄钢板给每台装置配一个外壳，已知薄钢板的面积有两种规格：甲种薄钢板每张面积2㎡，可做A、B的外壳分别为2个和7个，乙种薄钢板每张面积5㎡，可做A、B的外壳分别为7个和9个，求两种薄钢板各用多少张，才能使总的用料面积最小？

Answer 1

分析：设甲乙两种薄钢板各用x，y张，用料总面积为z，则目标函数为z=2x+5y，根据题设，确定约束条件，作出可行域，即可求得目标函数的最值．

解答：解：设甲乙两种薄钢板各用x，y张，用料总面积为z，则目标函数为z=2x+5y，…（2分）
约束条件为：

2x+7y≥41 7x+9y≥66 x≥0，y≥0 x，y∈N

                    …（5分）
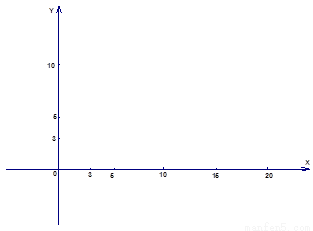
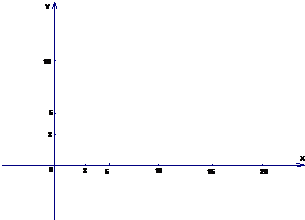
作出约束条件的可行域如图：

…（8分）
作直线l：2x+5y=0，平移，观察知，当l经过点M时，z取到最小值．…（10分）
解方程组

2x+7y=41 7x+9y=66

，得M点坐标为x=3，y=5       …（12分）
所以z_min=2x+5y=31㎡…（13分）
答：甲种钢板用3张，乙种钢板用5张，能够使总的用料面积最小． …（14分）

点评：本题考查函数模型的构建，考查利用数学知识解决实际问题，解题的关键是确定约束条件，作出可行域．