题目内容
已知椭圆![]() 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(Ⅰ)求过点O、F,并且与椭圆的左准线l相切的圆的方程;
(Ⅱ)设过点F且不与坐标轴垂直交椭圆于A、B两点,线段AB的垂直平分线与x轴交于点G,求点G横坐标的取值范围.

是解(1) ∵a2=2,b2=1,∴c=1,F(-1,0),l:x=-2.
∵圆过点O、F.
∴圆心M在直线x=-![]()
设M(-![]() ),则圆半径
),则圆半径
r=|(-![]() )-(-2)|=
)-(-2)|=![]() .
.
由|OM|=r,得
解得t=±![]() ,
,
∴所求圆的方程为(x+![]() )2+(y±
)2+(y±![]() ) 2=
) 2=![]() .
.
(2)设直线AB的方程为y=k(x+1)(k≠0),
代入![]() +y2=1,整理得(1+2k2)x2+4k2x+2k2-2=0.
+y2=1,整理得(1+2k2)x2+4k2x+2k2-2=0.
∵直线AB过椭圆的左焦点F,
∴方程有两个不等实根.
记A(x1,y1),B(x2,y2),AB中点N(x0,y0),
则x1+x2=-![]()
x0=![]()
![]()
![]() AB垂直平分线NG的方程为
AB垂直平分线NG的方程为![]()
令y=0,得
![]()
∵![]()
∴点G横坐标的取值范围为(![]() )
)

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案 名题金卷系列答案
名题金卷系列答案
相关题目
 的左焦点为F,O为坐标原点.
的左焦点为F,O为坐标原点.
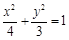 的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
的左焦点为F,过点F的直线交椭圆于A、B两点,线段AB的中点为G,AB的中垂线与x轴和y轴分别交于D、E两点.
 ,求直线AB的斜率;
,求直线AB的斜率; 的左焦点为F,左右顶点分别为A、C,
的左焦点为F,左右顶点分别为A、C, ,其中圆心P的坐标为
,其中圆心P的坐标为 .
. ,求
,求 上,求椭圆的方程.
上,求椭圆的方程. 的左焦点为F,右顶点为A,点B在椭圆上,且
的左焦点为F,右顶点为A,点B在椭圆上,且 轴,直线AB交
轴,直线AB交 轴于点P。若
轴于点P。若 ,则椭圆的离心率为
,则椭圆的离心率为