Question

（2013•安庆三模）如图，三棱柱ABC-A₁B₁C₁的侧棱与底面ABC垂直，底面ABC是等腰直角三角形，∠ACB=90°，侧棱AA₁=2，D、E分别是CC₁与A₁B的中点，点E在平面ABD上的射影是△ABD的垂心G
（1）求证：AD⊥A₁B；
（2）求A₁B与平面ABD所成角的大小．

Answer 1

分析：（Ⅰ）直接利用E在平面ABD上的射影是G，连结BG，可证AD垂直于平面BEG，则结论得证；
（Ⅱ）以C点为坐标原点，分别以射线CA为x轴、CB为y轴、CC₁为z轴建立空间直角坐标系，利用空间向量求A₁B与平面ABD所成角的大小．

解答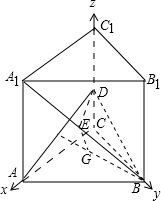：（Ⅰ）证明：如图，
∵点E在平面ABD上的射影是△ABD的垂心G．连结BG，则BG⊥AD，又EG⊥平面ABD，∴EG⊥AD
∴AD⊥平面BGE，∴AD⊥BE，即AD⊥A₁B．                  
（Ⅱ）解：以C点为坐标原点，分别以射线CA为x轴、CB为y轴、CC₁为z轴建立空间直角坐标系．
设点的坐标为A（a，0，0），则点B（0，a，0），A₁（a，0，2），D（0，0，1）．
由（Ⅰ）知AD⊥A₁B，又

AD

=(-a，0，1)，

BA1

=(a，-a，2)．
由

AD

•

BA1

=-a2+2=0，得a=

2

．
∴A(

2

，0，0)，B(0，

2

，0)，D（0，0，1），A1(

2

，0，2)．

AB

=(-

2

，

2

，0)，

AD

=(-

2

，0，1)，

BA1

=(

2

，-

2

，2)，
设平面ABD的一个法向量为

.

n

=(x，y，z)，
由

n • AB =0 n • AD =0

，得

- 2 x+ 2 y=0 - 2 x+z=0

，取z=

2

，得x=y=1．
所以

n

=(1，1，

2

)
故cos＜

n

，

BA1

＞=

n • BA1

| n |•| BA1 |

=

2 - 2 +2 2

2×2 2

=

1

2

，
所以A₁B与平面ABD所成角的为

π

6

．

点评：本题考查了直线与平面垂直的性质，考查了利用空间向量求直线和平面所成的角，考查了学生的空间想象和思维能力，解答的关键是理解平面的法向量与斜线上的向量所成角的余弦值与线面角的关系，是中档题．