题目内容
已知函数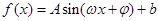 (
(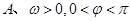 ,
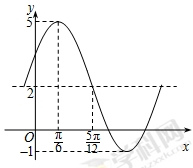
,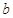 为常数)一段图像如图所示.
为常数)一段图像如图所示.
(1)求函数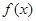 的解析式;
的解析式;
(2)将函数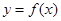 的图像向左平移
的图像向左平移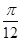 个单位,再将所得图像上各点的横坐标扩大为原来的4倍,得到函数
个单位,再将所得图像上各点的横坐标扩大为原来的4倍,得到函数 的图像,求函数
的图像,求函数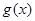 的单调递增区间.
的单调递增区间.
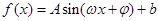 (
(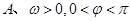 ,
,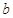 为常数)一段图像如图所示.
为常数)一段图像如图所示.
(1)求函数
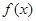 的解析式;
的解析式;(2)将函数
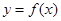 的图像向左平移
的图像向左平移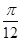 个单位,再将所得图像上各点的横坐标扩大为原来的4倍,得到函数
个单位,再将所得图像上各点的横坐标扩大为原来的4倍,得到函数 的图像,求函数
的图像,求函数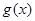 的单调递增区间.
的单调递增区间.(1)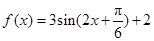 ;(2)
;(2)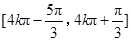 ,
,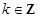
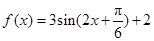 ;(2)
;(2)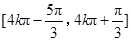 ,
,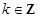
试题分析:(1)观察图像并由公式
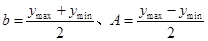 与
与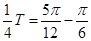 ,可计算出
,可计算出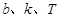 的值,然后由公式
的值,然后由公式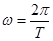 计算出
计算出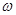 ,最后再由图像过点
,最后再由图像过点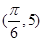 得到
得到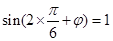 ,结合
,结合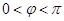 可确定
可确定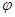 的值,从而确定函数
的值,从而确定函数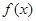 的解析式;(2)
的解析式;(2)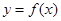 的图像向左平移得
的图像向左平移得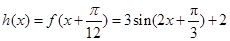 ,再将所得图像上各点的横坐标扩大为原来的4倍得到函数
,再将所得图像上各点的横坐标扩大为原来的4倍得到函数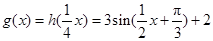 ,最后将
,最后将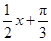 当作整体,由正弦函数的单调增区间可求出函数
当作整体,由正弦函数的单调增区间可求出函数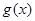 的单调增区间.
的单调增区间.试题解析:(1)由已知,
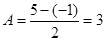 ,
,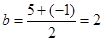 ,因为
,因为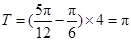 ,所以
,所以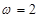
由“五点法”作图,
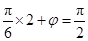 ,解得
,解得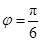
所以函数
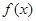 的解析式为
的解析式为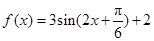 6分
6分(2)将函数
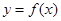 的图像向左平移
的图像向左平移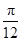 个单位后得到的函数解析式为
个单位后得到的函数解析式为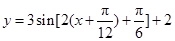 ,即
,即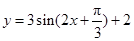 ,再将图像上各点的横坐标扩大为原来的4倍,得
,再将图像上各点的横坐标扩大为原来的4倍,得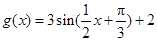
由
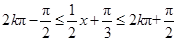 ,得
,得
故
 的单调递增区间为
的单调递增区间为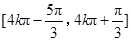 ,
,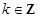 10分.
10分.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
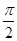 )的部分图象如图所示.
)的部分图象如图所示.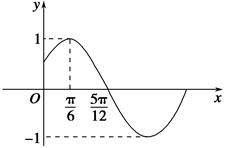
 的取值范围.
的取值范围. 的部分图象如图所示,为了得到g(x)=cos2x的图象,则只要将f(x)的图象( ).
的部分图象如图所示,为了得到g(x)=cos2x的图象,则只要将f(x)的图象( ).
 个单位长度
个单位长度 个单位长度
个单位长度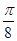 个单位长度
个单位长度 的最小正周期为 .
的最小正周期为 .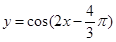 的图像向左平移
的图像向左平移 个单位,所得图像关于
个单位,所得图像关于 轴对称,则
轴对称,则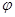 的最小值为
的最小值为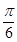
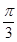
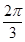
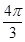
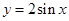 的图象先向右平移
的图象先向右平移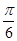 个单位,再将得到的图象上各点的横坐标变为原来的
个单位,再将得到的图象上各点的横坐标变为原来的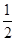 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数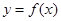 的图象,若
的图象,若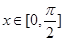 ,则函数
,则函数 的是( )
的是( )



 )图象的对称轴方程可以为( )
)图象的对称轴方程可以为( )


 (其中A>0,
(其中A>0,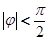 )的图象如图所示,为得到
)的图象如图所示,为得到 的图象,则只要将
的图象,则只要将 的图象( )
的图象( )
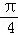 个单位长度
个单位长度 个单位长度
个单位长度 个单位长度
个单位长度