题目内容
已知关于x的不等式
x2+bx+c<0(ab>1)的解集为空集,则T=
+
的最小值为( )
| 1 |
| a |
| 1 |
| 2(ab-1) |
| a(b+2c) |
| ab-1 |
分析:由题意得:
>0,b2-
≤0,得c≥
.利用此式进行代换,将T化成T≥
,令ab-1=m,则m>0,利用基本不等式即可求出T的最小值.
| 1 |
| a |
| 4c |
| a |
| ab2 |
| 4 |
| 1+2ab+a2b2 |
| 2(ab-1) |
解答:解:由题意得:
>0,b2-
≤0,
得c≥
.
∴T=
+
≥
,
令ab-1=m,则m>0,
所以T≥
=
+
+2≥4.
则T=
+
的最小值为4.
故选D.
| 1 |
| a |
| 4c |
| a |
得c≥
| ab2 |
| 4 |
∴T=
| 1 |
| 2(ab-1) |
| a(b+2c) |
| ab-1 |
| 1+2ab+a2b2 |
| 2(ab-1) |
令ab-1=m,则m>0,
所以T≥
| 1+2(m+1)+(m+1)2 |
| 2m |
| m |
| 2 |
| 2 |
| m |
则T=
| 1 |
| 2(ab-1) |
| a(b+2c) |
| ab-1 |
故选D.
点评:本小题主要考查基本不等式、一元二次不等式的应用等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
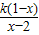 +1<0的解集为空集,求实数k的取值或取值范围.
+1<0的解集为空集,求实数k的取值或取值范围.