题目内容
设函数f(x)=
 +ax-lnx(a∈R).
+ax-lnx(a∈R).
(Ⅰ)当a=1时,求函数f(x)的极值;
(Ⅱ)当a≥2时,讨论函数f(x)的单调性;
(Ⅲ)若对任意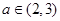 及任意
及任意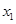 ,
, ∈[1,2],恒有
∈[1,2],恒有 成立,求实数m的取值范围.
成立,求实数m的取值范围.
(Ⅰ)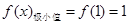 ,无极大值;(Ⅱ)当
,无极大值;(Ⅱ)当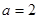 时,
时,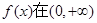 单调递减 ,当
单调递减 ,当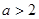 时,
时, 单调递减,在
单调递减,在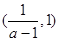 上单调递增;(Ⅲ)
上单调递增;(Ⅲ)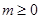 .
.
解析试题分析:(Ⅰ)当 时,求函数
时,求函数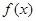 的极值,只需对函数
的极值,只需对函数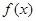 求导,求出导数等零点,及在零点两边的单调性,注意, 求函数
求导,求出导数等零点,及在零点两边的单调性,注意, 求函数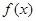 的极值不要忽略求函数的定义域;(Ⅱ)讨论函数
的极值不要忽略求函数的定义域;(Ⅱ)讨论函数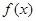 的单调性,只需判断
的单调性,只需判断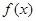 的导数
的导数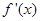 在区间上的符号,因此,此题先求导,在判断符号时,发现参数
在区间上的符号,因此,此题先求导,在判断符号时,发现参数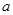 的取值对
的取值对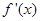 有影响,需对参数讨论,分
有影响,需对参数讨论,分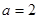 ,与
,与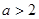 两种情况,从而确定单调区间;(Ⅲ)对任意
两种情况,从而确定单调区间;(Ⅲ)对任意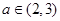 及任意
及任意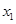 ,
, ∈[1,2],恒有
∈[1,2],恒有 成立,只需求出
成立,只需求出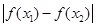 的最大值即可.
的最大值即可.
试题解析:(Ⅰ)函数的定义域为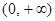 ,当
,当 时,
时, 令
令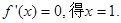 ,当
,当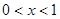 时,
时,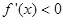 ;当
;当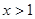 时,
时,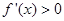 ,
,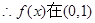 单调递减,在
单调递减,在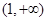 单调递增,
单调递增,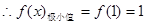 ,无极大值 ;
,无极大值 ;
(Ⅱ)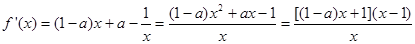
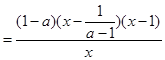
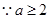 ,
,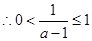 ,①当
,①当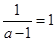 即
即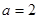 时,
时,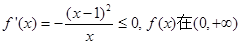 上是减函数,②当
上是减函数,②当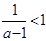 ,即
,即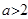 时,令
时,令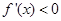 ,得
,得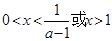 ,令
,令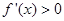 ,得
,得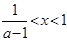
综上,当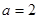 时,
时,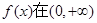 单调递减 ,当
单调递减 ,当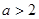 时,
时, 单调递减,在
单调递减,在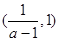 上单调递增;
上单调递增;
(Ⅲ)由(Ⅱ)知,当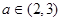 时,
时,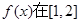 上单调递减,当
上单调递减,当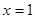 时,
时,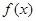 有最大值,当
有最大值,当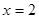 时,
时,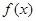 有最小值,
有最小值,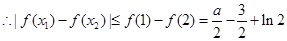 ,
,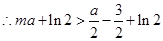 ,
,
而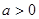 经整理得
经整理得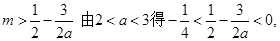
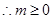 .
.
考点:函数与导数,导数与函数的单调性、导数与函数的极值,导数与不等式的综合应用,考查学生的基本推理能力,考查学生的基本运算能力以及转化与化归的能力.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
 和
和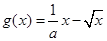 ,且
,且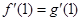 .
. ,
, 的表达式;
的表达式;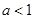 时,不等式
时,不等式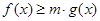 在
在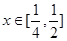 上恒成立,求实数
上恒成立,求实数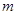 的取值范围.
的取值范围. ,
,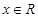 .
.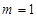 ,
,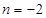 时,求
时,求 的单调区间;
的单调区间;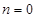 ,且
,且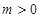 时,求
时,求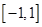 上的最大值.
上的最大值.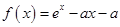 .
.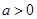 ,
,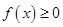 对一切
对一切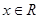 恒成立,求
恒成立,求 的最大值;
的最大值;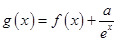 ,且
,且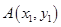 、
、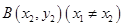 是曲线
是曲线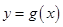 上任意两点,若对任意
上任意两点,若对任意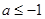 ,直线
,直线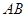 的斜率恒大于常数
的斜率恒大于常数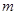 ,求
,求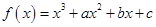 ,曲线
,曲线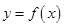 在点
在点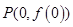 处的切线是
处的切线是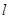 :
: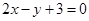
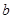 ,
,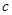 的值;
的值; 在
在 上单调递增,求
上单调递增,求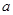 的取值范围
的取值范围  -lnx,x∈[1,3].
-lnx,x∈[1,3].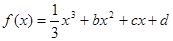 ,设曲线
,设曲线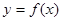 在与
在与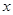 轴交点处的切线为
轴交点处的切线为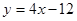 ,
,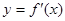 为
为 的导函数,满足
的导函数,满足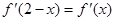 .
.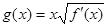 ,
,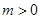 ,求函数
,求函数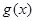 在
在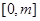 上的最大值;
上的最大值;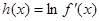 ,若对于一切
,若对于一切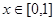 ,不等式
,不等式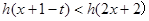 恒成立,求实数
恒成立,求实数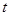 的取值范围.
的取值范围.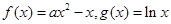 .
.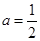 ,求函数
,求函数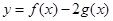 的极值,
的极值, ,使得
,使得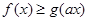 成立?若存在,求出实数
成立?若存在,求出实数 为实数,函数
为实数,函数
 的单调区间与极值;
的单调区间与极值; 且
且 时,
时,