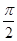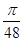题目内容
半径为1的球面上有 三点,其中点
三点,其中点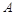 与
与 两点间的球面距离均为
两点间的球面距离均为 ,
, 两点间的球面距离为
两点间的球面距离为 ,则球心到平面
,则球心到平面 的距离为( )
的距离为( )
A. | B. | C.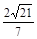 | D. |
B
解析试题分析:根据题意可知:球心O与A,B,C三点构成三棱锥O-ABC,且OA=OB=OC=R=1,∠AOB=∠AOC=90°,∠BOC=60°,故AO⊥面BOC.所以此题可以根据体积法求得球心O到平面ABC的距离. 解:球心O与A,B,C三点构成三棱锥O-ABC,如图所示,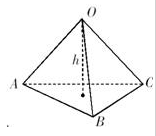
已知OA=OB=OC=R=1,∠AOB=∠AOC=90°,∠BOC=60°,由此可得AO⊥面BOC.∵S△BOC= ,S△ABC=
,S△ABC= .
.
∴由VA-BOC=VO-ABC,得 h= .故选B.
.故选B.
考点:点到面的距离, 球面距离
点评:本小题主要考查立体几何球面距离及点到面的距离、三棱锥的结构等基础知识,考查运算求解能力,考查空间想象力.属于基础题

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
火星的半径约是地球半径的一半,则地球的体积是火星的( )
| A.4倍 | B.8倍 | C. 倍 倍 | D. 倍 倍 |
一个几何体的三视图形状都相同,大小均相等,那么这个几何体不可以是( )
| A.球 | B.三棱锥 | C.正方体 | D.圆柱 |
一个三棱锥的三视图如图,则该三棱锥的体积为( )
A. | B. | C. | D. |
若 ,
, 是异面直线,
是异面直线, ,
, 也是异面直线,则
也是异面直线,则 与
与 的位置关系是
的位置关系是
| A.异面 | B.相交或平行 | C.平行或异面 | D.相交或平行或异面 |
长方体一个顶点上三条棱的长分别为3、4、5,且它的八个顶点都在同一球面上,这个球的表面积是( )
A.20 π π | B.25 π π | C.50π | D.200π |
 ,
, ,则
,则 两点间的球面距离为 ( )
两点间的球面距离为 ( )



 . 则
. 则 的外接圆的面积为
的外接圆的面积为


 ·
· =0,沿BD折成直二面角A一BD-C,且4AB2 +2BD2 =1,则三棱锥A-BCD的外接球的表面积为( )
=0,沿BD折成直二面角A一BD-C,且4AB2 +2BD2 =1,则三棱锥A-BCD的外接球的表面积为( )