题目内容
已知:等差数列{an}中,a3+a4=15,a2a5=54,公差d<0。
(1)求数列{an}的通项公式an;
(2)求数列的前n项和Sn的最大值及相应的n的值.
(1)求数列{an}的通项公式an;
(2)求数列的前n项和Sn的最大值及相应的n的值.
解:(1)
∴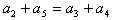 ,
,
∴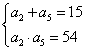 ,
,
解得: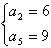 (因d<0,舍去)或
(因d<0,舍去)或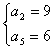 ,
,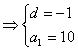 ,∴
,∴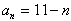 。
。
(2)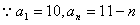 ,
,
∴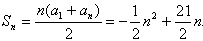 ,
,
又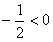 ,对称轴为
,对称轴为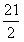 ,
,
故当n=10或11时,Sn取得最大值,其最大值为55。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知在等差数列{an}中,a1=120,d=-4,若Sn≤an(n≥2),则n的最小值为( )
| A、60 | B、62 | C、70 | D、72 |