题目内容
口袋内有n(n>3)个大小相同的球,其中有3个红球和n-3个白球,已知从口袋中随机取出一个球是红球的概率是p,且6p∈N.若有放回地从口袋中连续地取四次球(每次只取一个球),在四次取球中恰好取到两次红球的概率大于
(Ⅰ)求p和n;
(Ⅱ)不放回地从口袋中取球(每次只取一个球),取到白球时即停止取球,记ξ为第一次取到白球时的取球次数,求ξ的分布列和期望Eξ.
| 8 | 27 |
(Ⅰ)求p和n;
(Ⅱ)不放回地从口袋中取球(每次只取一个球),取到白球时即停止取球,记ξ为第一次取到白球时的取球次数,求ξ的分布列和期望Eξ.
分析:(Ⅰ)利用二项分布的概率计算公式即可得出;
(Ⅱ)利用相互独立事件的概率计算公式、离散型随机变量的分布列及其数学期望即可得出.
(Ⅱ)利用相互独立事件的概率计算公式、离散型随机变量的分布列及其数学期望即可得出.
解答:解:(Ⅰ)由题设可知:
p2(1-p)2>
,
∵p(1-p)>0,∴不等式可化为p(1-p)>
,
解不等式得
<p<
,即2<6p<4,
又∵6p∈N,∴6p=3,∴p=
.
∴p=
,∴
=
,解得n=6.
(Ⅱ)由(Ⅰ)可知:n=6.
ξ可取1,2,3,4.
∵P(ξ=1)=
=
,P(ξ=2)=
×
=
,
P(ξ=3)=
×
×
=
,P(ξ=4)=
×
×
×
=
.
∴ξ的分布列为
∴Eξ=1×
+2×
+3×
+4×
=
.
| C | 2 4 |
| 8 |
| 27 |
∵p(1-p)>0,∴不等式可化为p(1-p)>
| 2 |
| 9 |
解不等式得
| 1 |
| 3 |
| 2 |
| 3 |

又∵6p∈N,∴6p=3,∴p=
| 1 |
| 2 |
∴p=
| 1 |
| 2 |
| 3 |
| n |
| 1 |
| 2 |
(Ⅱ)由(Ⅰ)可知:n=6.
ξ可取1,2,3,4.
∵P(ξ=1)=
| ||
|
| 1 |
| 2 |
| ||
|
| ||
|
| 3 |
| 10 |
P(ξ=3)=
| ||
|
| ||
|
| ||
|
| 3 |
| 20 |
| ||
|
| ||
|
| ||
|
| ||
|
| 1 |
| 20 |
∴ξ的分布列为
∴Eξ=1×
| 1 |
| 2 |
| 3 |
| 20 |
| 3 |
| 20 |
| 1 |
| 20 |
=
| 7 |
| 4 |
点评:熟练掌握二项分布的概率计算公式、相互独立事件的概率计算方法、离散型随机变量的分布列及其数学期望是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
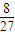
 时,不放回地从口袋中随机取出3个球,求取到白球的个数ξ的期望Eξ;
时,不放回地从口袋中随机取出3个球,求取到白球的个数ξ的期望Eξ; ,求p和n.
,求p和n. 时,不放回地从口袋中随机取出3个球,求取到白球的个数ξ的期望Eξ;
时,不放回地从口袋中随机取出3个球,求取到白球的个数ξ的期望Eξ;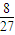 ,求p和n.
,求p和n.