题目内容
(2012•大连模拟)一个口袋内有n(n>3)个大小相同的球,其中有3个红球和(n-3)个白球.已知从口袋中随机取出一个球是红球的概率是p.
(I)当p=
时,不放回地从口袋中随机取出3个球,求取到白球的个数ξ的期望Eξ;
(II)若6p∈N,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
,求p和n.
(I)当p=
| 3 |
| 5 |
(II)若6p∈N,有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
| 8 |
| 27 |
分析:(I)根据p=
,可知5个球中有2个白球,故白球的个数ξ可取0,1,2,求出相应的概率,即可求得期望,或依题意ξ服从参数为N=5,M=2,n=3的超几何分布,可求期望;
(II)根据有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
建立不等式
p2(1-p)2>
,从而可求求p和n.
| 3 |
| 5 |
(II)根据有放回地从口袋中连续地取四次球(每次只取一个球),在四次摸球中恰好取到两次红球的概率大于
| 8 |
| 27 |
| C | 2 4 |
| 8 |
| 27 |
解答:解:(I)p=
⇒
=
⇒n=5,所以5个球中有2个白球
故白球的个数ξ可取0,1,2.(1分)
p(ξ=0)=
=
,p(ξ=1)=
=
,p(ξ=2)=
=
.(4分)
Eξ=
×0+
×1+
×2=
.(6分)
(另解:依题意ξ服从参数为N=5,M=2,n=3的超几何分布,所以Eξ=
×3=
.
(II)由题设知,
p2(1-p)2>
,(8分)
因为p(1-p)>0,所以不等式可化为p(1-p)>
,
解不等式得,
<p<
,即2<6p<4.(10分)
又因为6p∈N,所以6p=3,即p=
,
所以p=
,所以
=
,所以n=6.(12分)
| 3 |
| 5 |
| 3 |
| n |
| 3 |
| 5 |
故白球的个数ξ可取0,1,2.(1分)
p(ξ=0)=
| ||
|
| 1 |
| 10 |
| ||||
|
| 3 |
| 5 |
| ||||
|
| 3 |
| 10 |
Eξ=
| 1 |
| 10 |
| 3 |
| 5 |
| 3 |
| 10 |
| 6 |
| 5 |
(另解:依题意ξ服从参数为N=5,M=2,n=3的超几何分布,所以Eξ=
| 2 |
| 5 |
| 6 |
| 5 |
(II)由题设知,
| C | 2 4 |
| 8 |
| 27 |
因为p(1-p)>0,所以不等式可化为p(1-p)>
| 2 |
| 9 |
解不等式得,
| 1 |
| 3 |
| 2 |
| 3 |
又因为6p∈N,所以6p=3,即p=
| 1 |
| 2 |
所以p=
| 1 |
| 2 |
| 3 |
| n |
| 1 |
| 2 |
点评:本题考查离散型随机变量的分布列和期望,考查解不等式,解题的关键是明确变量的取值与含义.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
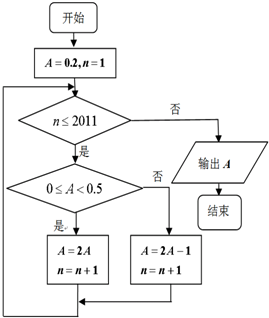 (2012•大连模拟)已知某程序框图如图所示,则该程序运行后,输出的结果为( )
(2012•大连模拟)已知某程序框图如图所示,则该程序运行后,输出的结果为( )