题目内容
15.在平面直角坐标系中,直线l:$\left\{\begin{array}{l}x=3+t\\ y=3-2t\end{array}$(t是参数,t∈R),圆C:$\left\{\begin{array}{l}x=2cosθ\\ y=2+2sinθ\end{array}$(θ是参数,θ∈[0,2π)),则圆心到直线的距离是$\frac{7\sqrt{5}}{5}$.分析 直接把直线的参数方程和圆的参数方程转化为直角坐标方程,进一步利用点到直线的距离公式求出结果.
解答 解:直线l:$\left\{\begin{array}{l}x=3+t\\ y=3-2t\end{array}$(t是参数,t∈R),
转化成直角坐标方程为:2x+y-9=0,
圆C:$\left\{\begin{array}{l}x=2cosθ\\ y=2+2sinθ\end{array}$(θ是参数,θ∈[0,2π)),
转化成直角坐标方程为:x2+(y-2)2=4,
则圆心到直线的距离d=$\frac{|2-9|}{\sqrt{5}}=\frac{7\sqrt{5}}{5}$.
故答案为:$\frac{7\sqrt{5}}{5}$.
点评 本题考查的知识要点:参数方程与直角坐标方程的互化,点到直线的距离的应用,主要考查学生的应用能力.

练习册系列答案
相关题目
7.多面体MN-ABCD的底面ABCD矩形,其正(主)视图和侧(左)视图如图,其中正(主)视图为等腰梯形,侧(左)视图为等腰三角形,则该多面体的体积为( )
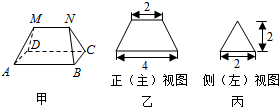

| A. | $\frac{16}{3}$ | B. | $\sqrt{6}$ | C. | $\frac{20}{3}$ | D. | 6 |
