题目内容
在长方体ABCD-A1B1C1D1中,AB=1,AD=2.若存在各棱长均相等的四面体P1P2P3P4,其中P1,P2,P3,P4分别在棱AB,A1B1,C1D1,CD所在的直线上,则此长方体的体积为 .
4
解析试题分析:若各棱长均相等的四面体P1P2P3P4,其中P1,P2,P3,P4分别在棱AB,A1B1,C1D1,CD所在的直线上,
则棱AB,A1B1,C1D1,CD所在的直线应为某正四棱柱的四条侧棱所在的直线
∵AD=2,
∴A1A=2
故此长方体的体积V=2×2×1=4
考点:棱柱、棱锥、棱台的体积.
点评:本题考查的知识点是棱柱的几何特征,棱锥的几何特征,其中根据正四面体是由正方体截掉四个角得到的,分析出A1A=AD,是解答的关键.

练习册系列答案
相关题目
 ,则线段
,则线段 的长度是
的长度是  的底面是正六边形,
的底面是正六边形, ,则直线
,则直线 所成的角为
所成的角为 
 ,
, 是两条直线,且
是两条直线,且 不垂直于平面
不垂直于平面 ,那么平面
,那么平面 是异面直线,则直线
是异面直线,则直线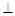 底面ABCD,则下列结论中正确的是 (把正确的答案都填上)
底面ABCD,则下列结论中正确的是 (把正确的答案都填上)
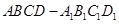 中,二面角
中,二面角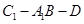 的余弦值为 .
的余弦值为 . 垂直平行四边形
垂直平行四边形 所在平面,若
所在平面,若 ,则平行四边形
,则平行四边形 (填形状)
(填形状) 处,乙站在水坝斜面上的点
处,乙站在水坝斜面上的点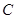 处,已知测得从
处,已知测得从 到库底与水坝的交线的距离分别为
到库底与水坝的交线的距离分别为 米、
米、 米,
米, 的长为
的长为 米,
米, 的长为
的长为 米,则库底与水坝所成的二面角的大小 度.
米,则库底与水坝所成的二面角的大小 度.
