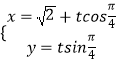Question

【题目】设函数是定义在上的偶函数，且对任意的恒有，已知当时，，则下列命题：

①对任意，都有；②函数在上递减，在上递增；

③函数的最大值是1，最小值是0；④当时，.

其中正确命题的序号有________．

Answer 1

【答案】①②④

【解析】

根据已知，分析出函数的周期性，单调性，最值，函数解析式，逐一分析四个命题的真假，可得答案．

①∵,∴f（x+2）=f[（x+1）-1]=f（x），∴2是函数f（x）的一个周期，正确；②当时，为增函数，故x∈[-1，0]时，f（x）为减函数，由函数的周期性可得f（x）在（1，2）上是减函数，在（2，3）上是增函数，正确；③由解析式可知函数取最小值，取最大值1，故错误；④设x∈（3,4），则4-x∈（0,1），f（4-x）==f（-x）=f（x），故正确；

故答案为：①②④.