题目内容
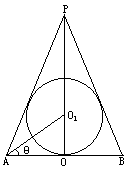
如图,设球的半径为R,联系已知球半径、锥底半径和母线来表达外切于这个球的一切圆锥中全面积最小的圆锥的全面积.
答案:
解析:
提示:
解析:
|
|
提示:
|
球的半径是定值,但这个球的外切圆锥是相当自由的概念,锥高h>2R,可大可小,锥底半径也随着锥高的变化而变化,如何选择一个恰当的自变量,可以互相兼顾,比较方便地勾勒出这些量,从而把外切圆锥的全面积表示为这个变量的函数,然后来求全面积这个目标函数的最小值,是一个很重要的问题.经过多方试探,这里给出一种选用∠OAC= |

练习册系列答案
相关题目

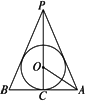
 如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2,
如图,在三棱锥S-ABC中,侧面SAB⊥底面ABC,且∠ASB=∠ABC=90°,AS=SB=2, C.
C.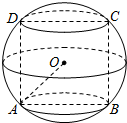 如图,半径R=3的球O中有一内接圆柱,设圆柱的高为h,底面半径为r.
如图,半径R=3的球O中有一内接圆柱,设圆柱的高为h,底面半径为r. 的半径为R,内切于顶点为P的圆锥(轴截面如图).设∠
的半径为R,内切于顶点为P的圆锥(轴截面如图).设∠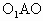 =θ.
=θ.