题目内容
若椭圆 的左、右焦点分别为F1、F2,抛物线y2=2bx的焦点为F.若
的左、右焦点分别为F1、F2,抛物线y2=2bx的焦点为F.若 ,则此椭圆的离心率为
,则此椭圆的离心率为
- A.

- B.

- C.

- D.

B
分析:先根据椭圆和抛物线的方程分别求得其焦点坐标,进而分别表示出 ,根据
,根据 建立等式求得b和c的关系,进而求得a和c的关系,则椭圆的离心率可得.
建立等式求得b和c的关系,进而求得a和c的关系,则椭圆的离心率可得.
解答:依题意可知抛物线的焦点为( ,0),椭圆的焦点为(
,0),椭圆的焦点为( ,0),(-
,0),(- ,0)
,0)
∵ ,
,
∴ +
+ =3(
=3( -
- ),整理得b=c
),整理得b=c
∴a=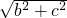 =
= c
c
∴e= =
=
故选B
点评:本题主要考查了椭圆和抛物线的简单性质.考查了学生基础知识的理解和应用以及基本的运算能力.
分析:先根据椭圆和抛物线的方程分别求得其焦点坐标,进而分别表示出
 ,根据
,根据 建立等式求得b和c的关系,进而求得a和c的关系,则椭圆的离心率可得.
建立等式求得b和c的关系,进而求得a和c的关系,则椭圆的离心率可得.解答:依题意可知抛物线的焦点为(
 ,0),椭圆的焦点为(
,0),椭圆的焦点为( ,0),(-
,0),(- ,0)
,0)∵
 ,
,∴
 +
+ =3(
=3( -
- ),整理得b=c
),整理得b=c∴a=
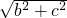 =
= c
c∴e=
 =
=
故选B
点评:本题主要考查了椭圆和抛物线的简单性质.考查了学生基础知识的理解和应用以及基本的运算能力.

练习册系列答案
相关题目


 (本小题满分12分) 已知椭圆
(本小题满分12分) 已知椭圆
 的左、右焦点分别是
的左、右焦点分别是 、
、 ,
, 是椭圆右准线上的一点,线段
是椭圆右准线上的一点,线段 的垂直平分线过点
的垂直平分线过点 :
: 按向量
按向量 平移后的直线是
平移后的直线是 ,直线
,直线 :
: 按向量
按向量 平移后的直线是
平移后的直线是 (其中
(其中 )。
)。 的取值范围。
的取值范围。 时,求椭圆的方程。
时,求椭圆的方程。 、
、 两点,
两点, 、
、 两点。求四边形ABCD面积
两点。求四边形ABCD面积 的取值范围。
的取值范围。