题目内容
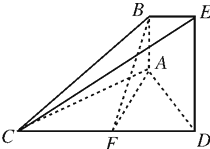
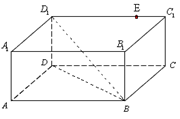
如图,已知多面体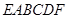 的底面
的底面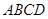 是边长为
是边长为 的正方形,
的正方形,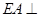 底面
底面 ,
, ,且
,且 .
.
(Ⅰ )求多面体 的体积;
的体积;
(Ⅱ )求证:平面EAB⊥平面EBC;
(Ⅲ)记线段CB的中点为K,在平面 内过K点作一条直线与平面
内过K点作一条直线与平面 平行,要求保留作图痕迹,但不要求证明.
平行,要求保留作图痕迹,但不要求证明.
(Ⅰ)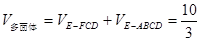 . (Ⅱ )见解析.(Ⅲ)利用三角形中位线定理,取线段DC的中点
. (Ⅱ )见解析.(Ⅲ)利用三角形中位线定理,取线段DC的中点 ,连接即为所求.
,连接即为所求.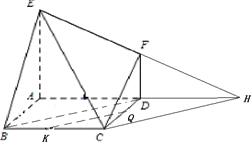
解析试题分析:(Ⅰ)连接ED,利用“分割法”计算得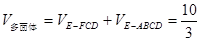 .(Ⅱ )根据ABCD为正方形,得到AB⊥BC. 利用EA⊥平面ABCD,得到BC⊥EA. 证得BC⊥平面EAB.
.(Ⅱ )根据ABCD为正方形,得到AB⊥BC. 利用EA⊥平面ABCD,得到BC⊥EA. 证得BC⊥平面EAB.
根据BC?平面EBC,得到平面EAB⊥平面EBC.(Ⅲ)取线段DC的中点 ;连接
;连接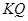 ,则直线
,则直线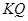 即为所求.
即为所求.
试题解析:(Ⅰ)如图,连接ED,
∵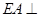 底面
底面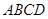 且
且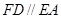 ,∴
,∴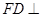 底面
底面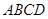
∴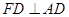
∵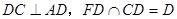
∴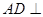 面
面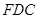 1分
1分
∴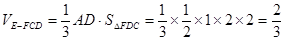 2分
2分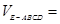
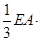
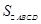
 3分
3分
∴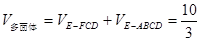 . 5分
. 5分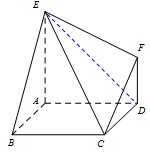
(Ⅱ )∵ABCD为正方形,∴AB⊥BC. 6分
∵EA⊥平面ABCD,BC?平面ABCD,
∴BC⊥EA. 7分
又AB∩EA=A,∴BC⊥平面EAB. 8分
又∵BC?平面EBC,
∴平面EAB⊥平面EBC. 10分
(Ⅲ)取线段DC的中点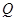 ;连接
;连接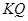 ,则直线
,则直线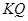 即为所求. 11分
即为所求. 11分
图上有正确的作图痕迹 12分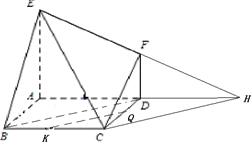
考点:1、平行关系,2、垂直关系,3、体积计算.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 的底面是直角梯形,
的底面是直角梯形, ,
, ,
,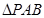 和
和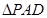 是两个边长为
是两个边长为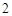 的正三角形,
的正三角形,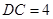 ,
, 为
为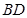 的中点,
的中点,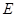 为
为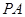 的中点.
的中点.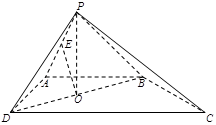
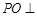 平面
平面 ;
;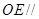 平面
平面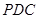 ;
;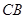 与平面
与平面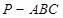 中,
中,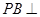 底面
底面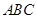 ,
,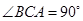 ,
,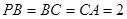 ,
,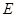 为
为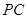 的中点,点
的中点,点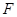 在
在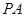 上,且
上,且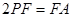 .
.
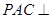 平面
平面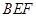 ;
;  与平面
与平面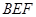 所成的二面角的平面角(锐角)的余弦值.
所成的二面角的平面角(锐角)的余弦值.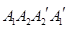 ,满足
,满足 在
在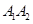 上,
上,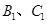 在
在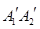 上,且
上,且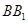 ∥
∥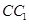 ∥
∥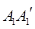 ,
,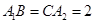 ,
,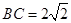 ,
,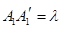 ,沿
,沿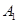 与
与 、
、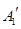 与
与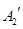 重合后分别记为
重合后分别记为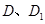 ,在直三棱柱
,在直三棱柱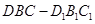 中,点
中,点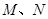 分别为
分别为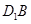 和
和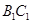 的中点.
的中点.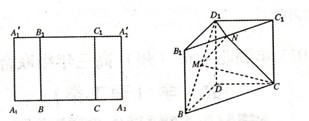
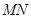 ∥平面
∥平面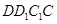 ;
;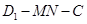 为直二面角,求
为直二面角,求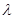 的值.
的值.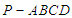 中,底面
中,底面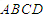 为菱形,
为菱形,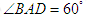 ,
,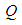 为
为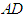 的中点。
的中点。
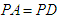 ,求证:平面
,求证:平面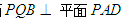 ;
;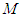 在线段
在线段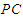 上,
上,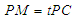 ,试确定
,试确定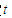 的值,使
的值,使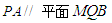 ;
;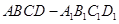 中,底面
中,底面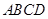 为正方形,
为正方形,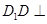 面
面 ,
,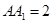 ,点
,点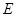 在棱
在棱 上,且
上,且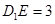 .
.
 上确定一点
上确定一点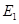 ,使得直线
,使得直线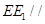 平面
平面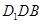 ,并证明;
,并证明; 在底面
在底面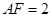 ,请说明点
,请说明点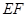 长度的最小值.
长度的最小值.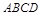 为梯形,
为梯形,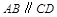 ,
,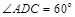 ,四边形
,四边形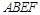 为矩形,且平面
为矩形,且平面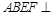 平面
平面 ,点
,点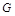 为
为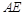 的中点.
的中点.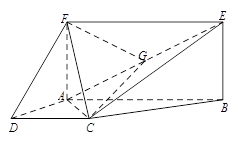
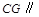 平面
平面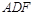 ;
;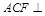 平面
平面 ;
;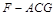 的体积.
的体积.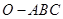 的侧棱
的侧棱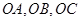 两两垂直,且
两两垂直,且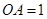 ,
,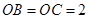 ,
, 是
是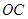 的中点.(1)求
的中点.(1)求 点到面
点到面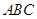 的距离;(2)求二面角
的距离;(2)求二面角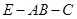 的正弦值.
的正弦值.