��Ŀ����
15����֪����{an}��ǰn���ΪSn������$\overrightarrow{a}$=��Sn��1����$\overrightarrow{b}$=��2n-1��$\frac{1}{2}$������������$\overrightarrow{a}$��$\overrightarrow{b}$����1��������{an}��ͨ�ʽ��
��2���躯��f��x��=��$\frac{1}{2}$��x������{bn}��������b1=1��f��bn+1��=$\frac{1}{{f��-{b_n}-1��}}$��
��������{bn}��ͨ�ʽ��
����cn=$\frac{{b}_{n}}{{a}_{n}}$��������{cn}��ǰn���Tn��
���� ��1�������������ߵ������ʾ���ɵ�Sn=2n+1-2�����ɵ�n��1ʱ��an=Sn-Sn-1��n=1ʱ��a1=S1�����ɵõ�����ͨ�ʽ��
��2��������ָ�����������ʺ͵Ȳ����еĶ��壬���ɵõ�����ͨ�ʽ��
�����Cn=$\frac{{b}_{n}}{{a}_{n}}$=$\frac{n}{{2}^{n}}$���������е���ͷ�������λ���������ϵȱ����е����ʽ�������������ɵõ�����ͣ�
��� �⣺��1��������$\overrightarrow{a}$=��Sn��1����$\overrightarrow{b}$=��2n-1��$\frac{1}{2}$����$\overrightarrow{a}$��$\overrightarrow{b}$��
�ɵ�$\frac{1}{2}$Sn=2n-1����Sn=2n+1-2��
��n��1ʱ��an=Sn-Sn-1=��2n+1-2��-��2n-2��=2n��
��n=1ʱ��a1=S1=2��������ʽ��
��������{an}��ͨ�ʽΪan=2n��n��N*��
��2����f��x��=��$\frac{1}{2}$��x��b1=1��f��bn+1��=$\frac{1}{{f��-{b_n}-1��}}$��
�ɵã�$\frac{1}{2}$��${\;}^{{b}_{n+1}}$=$\frac{1}{��\frac{1}{2}��^{-1-{b}_{n}}}$=��$\frac{1}{2}$��${\;}^{1+{b}_{n}}$��
����bn+1=bn+1���ɵ�{bn}Ϊ��������Ϊ1�ĵȲ����У�
����bn=n��
��Cn=$\frac{{b}_{n}}{{a}_{n}}$=$\frac{n}{{2}^{n}}$��ǰn���Tn=1•$\frac{1}{2}$+2•��$\frac{1}{2}$��2+��+��n-1��•��$\frac{1}{2}$��n-1+n•��$\frac{1}{2}$��n��
$\frac{1}{2}$Tn=1•��$\frac{1}{2}$��2+2•��$\frac{1}{2}$��3+��+��n-1��•��$\frac{1}{2}$��n+n•��$\frac{1}{2}$��n+1��
����ɵã�$\frac{1}{2}$Tn=$\frac{1}{2}$+��$\frac{1}{2}$��2+��+��$\frac{1}{2}$��n-1+��$\frac{1}{2}$��n-n•��$\frac{1}{2}$��n+1
=$\frac{\frac{1}{2}��1-\frac{1}{{2}^{n}}��}{1-\frac{1}{2}}$-n•��$\frac{1}{2}$��n+1��
����ɵã�ǰn���Tn=2-$\frac{n+2}{{2}^{n}}$��
���� ���⿼��Ȳ����е�ͨ�����ע���������е�ͨ������͵Ĺ�ϵ���������е���ͷ�������λ�������ͬʱ�����������ߵ������ʾ�͵ȱ����е����ʽ�����ã������е��⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�| A�� | -24 | B�� | 24 | C�� | -24$\sqrt{3}$ | D�� | 24$\sqrt{3}$ |
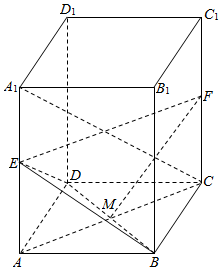 ��ͼ������סABCD-A1B1C1D1�У���E��A1A�ϵĵ㣬M��AC��BD�Ľ��㣮
��ͼ������סABCD-A1B1C1D1�У���E��A1A�ϵĵ㣬M��AC��BD�Ľ��㣮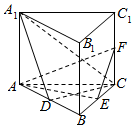 ��ͼ��ֱ������ABC-A1B1C1�ĵ���Ϊ�������Σ�E��F�ֱ���BC��CC1���е㣮
��ͼ��ֱ������ABC-A1B1C1�ĵ���Ϊ�������Σ�E��F�ֱ���BC��CC1���е㣮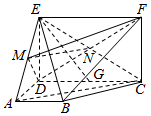 ��ͼ������CDEF������ABCD���ഹֱ����BAD=��ADC=90�㣬AB=AD=$\frac{1}{2}$CD��BE��DF��
��ͼ������CDEF������ABCD���ഹֱ����BAD=��ADC=90�㣬AB=AD=$\frac{1}{2}$CD��BE��DF��