题目内容
如图所示,在第一象限由直线y=2x,y=
x和曲线y=
所围图形的面积为 .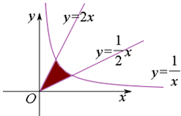
| 1 |
| 2 |
| 1 |
| x |

分析:先求出交点坐标,利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可.
解答:解:由
,x>0,解得
;
由
,x>0,解得
∴在第一象限由直线y=2x,y=
x和曲线y=
所围图形的面积为
2xdx+
dx-
dx=x2
+lnx
+
x2
=ln2.
故答案为:ln2.
|
|
由
|
|
∴在第一象限由直线y=2x,y=
| 1 |
| 2 |
| 1 |
| x |
| ∫ |
0 |
| ∫ |
|
| 1 |
| x |
| ∫ |
0 |
| x |
| 2 |
| | |
0 |
| | |
|
| 1 |
| 4 |
| | |
0 |
故答案为:ln2.
点评:本题考查了导数的运算法则、微积分基本定理的应用,考查了数形结合的思想,属于中档题.

练习册系列答案
相关题目
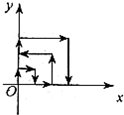 如图,一个粒子在第一象限运动,在第一秒末,它从原点运动到(0,1),接着它按如图所示的x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…),且每秒移动一个单位,那么第2008秒末这个粒子所处的位置的坐标为
如图,一个粒子在第一象限运动,在第一秒末,它从原点运动到(0,1),接着它按如图所示的x轴、y轴的平行方向来回运动,(即(0,0)→(0,1)→(1,1)→(1,0)→(2,0)→…),且每秒移动一个单位,那么第2008秒末这个粒子所处的位置的坐标为 如图所示,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线x=t(0≤t≤2)截这个三角形可得位于此直线左方的图形的面积为f(t),则函数y=f(t)的图象(如图所示)大致是
如图所示,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线x=t(0≤t≤2)截这个三角形可得位于此直线左方的图形的面积为f(t),则函数y=f(t)的图象(如图所示)大致是
 ,
, 和曲线
和曲线 所围图形的面积为 。
所围图形的面积为 。