题目内容
设椭圆C：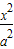
+
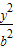=1（a＞b＞0）的左、右焦点分别为F1，F2，上顶点为A，过点A与AF2垂直的直线交x轴负半轴于点Q，且2
+
=
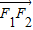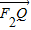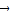．则椭圆C的离心率为 ．
【答案】分析：依题意可求得直线AQ的方程，从而求得Q点的坐标，利用向量的坐标运算由2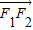
+
=
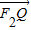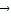可求得a，c之间的关系式，从而可求得椭圆C的离心率．
解答：解：∵A（0，b），F1（-c，0），F2（c，0），
∴直线AF2的斜率为：k=-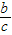
，
∵AQ⊥AF2，
∴kAQ=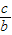
．
∴直线AQ的方程为：y-b=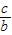
（x-0）=
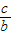x，
令y=0得：x=-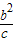
．
∴Q点的坐标为（-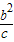
，0）．
∵2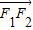
+
=
，
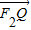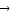∴2（2c，0）+（-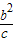
-c，0）=（0，0），
∴-
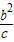=-3c，
∴3c2=b2=a2-c2，
∴
=
，
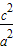∴e=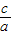
=
．
故答案为：
．
点评：本题考查椭圆的简单性质，考查向量的坐标运算，求得Q点的坐标是关键，属于中档题．
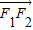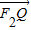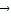+=可求得a，c之间的关系式，从而可求得椭圆C的离心率．解答：解：∵A（0，b），F1（-c，0），F2（c，0），
∴直线AF2的斜率为：k=-
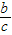，∵AQ⊥AF2，
∴kAQ=
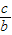．∴直线AQ的方程为：y-b=
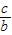（x-0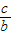）=x，令y=0得：x=-
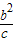．∴Q点的坐标为（-
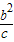，0）．∵2
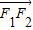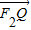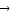+=，∴2（2c，0）+（-
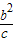-c，0）=（0，0），∴-
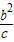=-3c，∴3c2=b2=a2-c2，
∴
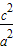=，∴e=
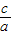=．故答案为：
．点评：本题考查椭圆的简单性质，考查向量的坐标运算，求得Q点的坐标是关键，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
+
=1（a＞b＞0）的左焦点为F1=（-
，0），椭圆过点P（-
，
）
=1（a＞b＞0）的左、右焦点分别为F1、F2，离心率为
，左焦点F1到直线l：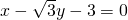
的距离等于长半轴长．
+
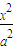=1（a＞b＞0）过点M（1，1），离心率e=
，O为坐标原点．
•
为定值．
设椭圆C：
+
=1（a＞b＞0）的左焦点为F，上顶点为A，过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q，且
=
．
y+3=0相切，求椭圆C的方程．
+
=1（a＞b＞0）的左焦点为F1=（-
，0），椭圆过点P（-
，
）