题目内容
设椭圆C: +
+ =1(a>b>0)的左焦点为F1=(-
=1(a>b>0)的左焦点为F1=(- ,0),椭圆过点P(-
,0),椭圆过点P(- ,
, )
)
(1)求椭圆C的方程;
(2)已知点D(l,0),直线l:y=kx+m与椭圆C交于A、B两点,以DA和DB为邻边的四边形是菱形,求k的取值范围.
解:(1)由题意知c= ,b2=a2-3,由
,b2=a2-3,由 +
+ =1得2a4-11a2+12=0,
=1得2a4-11a2+12=0,
所以(a2-4)(2a2-3)=0,得a2=4或a2= <c2(舍去),
<c2(舍去),
因此椭圆C的方程为 +y2=1.(4分)
+y2=1.(4分)
(2)由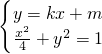 得(4k2+1)x2+8kmx+4(m2-1)=0.
得(4k2+1)x2+8kmx+4(m2-1)=0.
所以4k2+1>0,△═64k2m2-16(4k2+1)(m2-1)=64k2-16m+16>0,
得4k2+1>m2.①(6分)
设A(x1,y1),B(x2,y2),AB中点为M(x0,y0),则x1+x2=- ,x1•x2=
,x1•x2= ,
,
于是x0= ,y0=k•
,y0=k• +m=
+m= ,
,
∴M( ,
, ).
).
设菱形一条对角线的方程为y=- (x-1),则有x=-ky+1.
(x-1),则有x=-ky+1.
将点M的坐标代入,得- =
= +1,所以m=-
+1,所以m=- .②(9分)
.②(9分)
将②代入①,得4k2+1> ,
,
所以9k2>4k2+1,解得k∈(-∽, )∪(
)∪( ,+∞).(12分)
,+∞).(12分)
分析:(1)由题意知c= ,b2=a2-3,由
,b2=a2-3,由 +
+ =1得2a4-11a2+12=0,由此能求出椭圆C的方程.
=1得2a4-11a2+12=0,由此能求出椭圆C的方程.
(2)由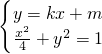 得(4k2+1)x2+8kmx+4(m2-1)=0.由△=64k2m2-16(4k2+1)(m2-1)=64k2-16m+16>0,得4k2+1>m2.设A(x1,y1),B(x2,y2),AB中点为M(x0,y0),由韦达定理知x1+x2=-
得(4k2+1)x2+8kmx+4(m2-1)=0.由△=64k2m2-16(4k2+1)(m2-1)=64k2-16m+16>0,得4k2+1>m2.设A(x1,y1),B(x2,y2),AB中点为M(x0,y0),由韦达定理知x1+x2=- ,x1•x2=
,x1•x2= ,于是x0=
,于是x0= ,y0=k•
,y0=k• +m=
+m= ,M(
,M( ,
, ).由此入手,能够求出k的取值范围.
).由此入手,能够求出k的取值范围.
点评:本题考查椭圆方程的求法和求k的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件.本题主要考查运算能力,比较繁琐,解题时要格外细心,避免出错.
 ,b2=a2-3,由
,b2=a2-3,由 +
+ =1得2a4-11a2+12=0,
=1得2a4-11a2+12=0,所以(a2-4)(2a2-3)=0,得a2=4或a2=
 <c2(舍去),
<c2(舍去),因此椭圆C的方程为
 +y2=1.(4分)
+y2=1.(4分)(2)由
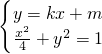 得(4k2+1)x2+8kmx+4(m2-1)=0.
得(4k2+1)x2+8kmx+4(m2-1)=0.所以4k2+1>0,△═64k2m2-16(4k2+1)(m2-1)=64k2-16m+16>0,
得4k2+1>m2.①(6分)
设A(x1,y1),B(x2,y2),AB中点为M(x0,y0),则x1+x2=-
 ,x1•x2=
,x1•x2= ,
,于是x0=
 ,y0=k•
,y0=k• +m=
+m= ,
,∴M(
 ,
, ).
).设菱形一条对角线的方程为y=-
 (x-1),则有x=-ky+1.
(x-1),则有x=-ky+1.将点M的坐标代入,得-
 =
= +1,所以m=-
+1,所以m=- .②(9分)
.②(9分)将②代入①,得4k2+1>
 ,
,所以9k2>4k2+1,解得k∈(-∽,
 )∪(
)∪( ,+∞).(12分)
,+∞).(12分)分析:(1)由题意知c=
 ,b2=a2-3,由
,b2=a2-3,由 +
+ =1得2a4-11a2+12=0,由此能求出椭圆C的方程.
=1得2a4-11a2+12=0,由此能求出椭圆C的方程.(2)由
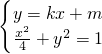 得(4k2+1)x2+8kmx+4(m2-1)=0.由△=64k2m2-16(4k2+1)(m2-1)=64k2-16m+16>0,得4k2+1>m2.设A(x1,y1),B(x2,y2),AB中点为M(x0,y0),由韦达定理知x1+x2=-
得(4k2+1)x2+8kmx+4(m2-1)=0.由△=64k2m2-16(4k2+1)(m2-1)=64k2-16m+16>0,得4k2+1>m2.设A(x1,y1),B(x2,y2),AB中点为M(x0,y0),由韦达定理知x1+x2=- ,x1•x2=
,x1•x2= ,于是x0=
,于是x0= ,y0=k•
,y0=k• +m=
+m= ,M(
,M( ,
, ).由此入手,能够求出k的取值范围.
).由此入手,能够求出k的取值范围.点评:本题考查椭圆方程的求法和求k的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件.本题主要考查运算能力,比较繁琐,解题时要格外细心,避免出错.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 =1(a>b>0)的左、右焦点分别为F1、F2,离心率为
=1(a>b>0)的左、右焦点分别为F1、F2,离心率为 ,左焦点F1到直线l:
,左焦点F1到直线l: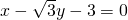 的距离等于长半轴长.
的距离等于长半轴长.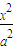 +
+ =1(a>b>0)过点M(1,1),离心率e=
=1(a>b>0)过点M(1,1),离心率e= ,O为坐标原点.
,O为坐标原点. •
• 为定值.
为定值. 设椭圆C:
设椭圆C: +
+ =1(a>b>0)的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且
=1(a>b>0)的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且 =
=
 .
. y+3=0相切,求椭圆C的方程.
y+3=0相切,求椭圆C的方程. +
+ =1(a>b>0)的左焦点为F1=(-
=1(a>b>0)的左焦点为F1=(- ,0),椭圆过点P(-
,0),椭圆过点P(- ,
, )
)