题目内容
给出下列命题:
①函数y=f(x)的图象与函数y=f(x-2)+3的图象一定不会重合;
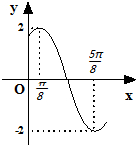
②函数y=log
(-x2+2x+3)的单调区间为(1,+∞);
③
(cosx+ex)dx=1-e-π;
④双曲线的渐近线方程是y=±
x,则该双曲线的离心率是
.
其中正确命题的序号是 (把你认为正确命题的序号都填上).
①函数y=f(x)的图象与函数y=f(x-2)+3的图象一定不会重合;
②函数y=log
| 1 |
| 2 |
③
| ∫ | 0 -π |
④双曲线的渐近线方程是y=±
| 3 |
| 4 |
| 5 |
| 4 |
其中正确命题的序号是
考点:命题的真假判断与应用
专题:函数的性质及应用,圆锥曲线的定义、性质与方程,概率与统计
分析:①,令f(x)=
x,g(x)=f(x-2)+3,整理可得g(x)=f(x),可判断①;
②,先求函数y=log
(-x2+2x+3)的定义域,再确定其单调区间,可判断②;
③,利用微积分基本定理计算
(cosx+ex)dx=1-e-π,可判断③;
④,双曲线的渐近线方程是y=±
x,则y=±
x=±
x或y=±
x=±
x,从而可求得则该双曲线的离心率,可判断④.
| 3 |
| 2 |
②,先求函数y=log
| 1 |
| 2 |
③,利用微积分基本定理计算
| ∫ | 0 -π |
④,双曲线的渐近线方程是y=±
| 3 |
| 4 |
| b |
| a |
| 3 |
| 4 |
| a |
| b |
| 3 |
| 4 |
解答:
解:对于①,令f(x)=
x,则g(x)=f(x-2)+3=
(x-2)+3=
x=f(x),此时函数y=f(x)的图象与函数y=f(x-2)+3的图象重合,故①错误;
对于②,由-x2+2x+3>0得:-1<x<3,所以函数y=log
(-x2+2x+3)的单调减区间为(-1,1),增区间为(1,3),故②错误;
对于③,
(cosx+ex)dx=(sinx+ex)
=1-e-π,故③正确;
对于④,双曲线的渐近线方程是y=±
x,则该双曲线的离心率e=
=
或e=
=
,故④错误.
故答案为:③.
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
对于②,由-x2+2x+3>0得:-1<x<3,所以函数y=log
| 1 |
| 2 |
对于③,
| ∫ | 0 -π |
| | | 0 -π |
对于④,双曲线的渐近线方程是y=±
| 3 |
| 4 |
| ||
| 4 |
| 5 |
| 4 |
| ||
| 3 |
| 5 |
| 3 |
故答案为:③.
点评:本题考查命题的真假判断与应用,综合考查函数的平移变换、复合函数的单调性、微积分基本定理的应用及双曲线的几何性质,考查转化思想.

练习册系列答案
相关题目
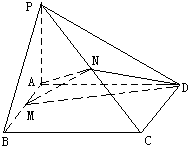 已知:ABCD是矩形,设PA=a,PA⊥平面ABCD,M,N分别是AB,PC的中心点.
已知:ABCD是矩形,设PA=a,PA⊥平面ABCD,M,N分别是AB,PC的中心点. 已知四面体O-ABC中,M、N分别是OA、BC的中点,P是MN上(靠近点M)的三等分点,其中OA=OB=OC=1,∠AOC=∠AOB=∠BOC=60°,求异面直线OP与AB所成角的余弦值.(用向量法)
已知四面体O-ABC中,M、N分别是OA、BC的中点,P是MN上(靠近点M)的三等分点,其中OA=OB=OC=1,∠AOC=∠AOB=∠BOC=60°,求异面直线OP与AB所成角的余弦值.(用向量法)